背景
兔子出生后两个月就能生小兔子,如果每月生一次且恰好生一对小兔子(雌性各一只),且出生的兔子都能成活。试问:由一对小兔子开始,一年后有多少对兔子,两年后呢?
【问题分析】
当前记为第0个月,有1对小兔子;第1个月初还是一对(成年)兔子;第2个月月初,这对成年兔子生了一对小兔子,共2对小兔子;第3个月月初,幼兔1对,成年兔子继续生1对小兔子,也即是说第3月月初有3对兔子;第4月月初成年兔子2对各生1对小兔子,上月出生的小兔子1对,共5对小兔子;…
【模型假设】
- 没有资源限制,兔子数量可以自由增长
- 没有死亡,兔子数量只增不减
- 初始兔子数量为1
【符号说明】
t:时间,单位:月,t=0,1,2,…;
Ft:第t时间段兔子的总数量,单位(对)
【建立模型】
第t个月月初的兔子总数量=第t个月月初幼兔子的数量+第t个月月初成年兔子的数量
=第t-2个月月初兔子的总数量+第t-1个月月初兔子的总数量
由此可得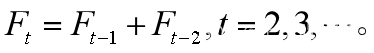 于是得到一个二阶常系数线性其次差分方程
于是得到一个二阶常系数线性其次差分方程![]() 【25】
【25】
其特征方程有两个不同实根 所以此方程的通解为
所以此方程的通解为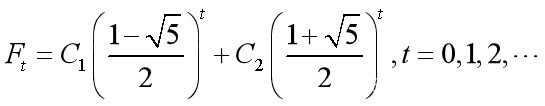
由于F0=F1=1,求解得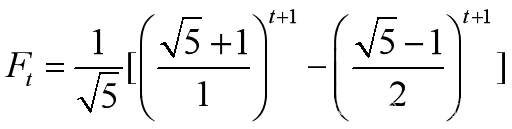 【26】【26】就是兔子数量随着月份变化而变化的表达式,又称为Fibonacci数列的卢卡斯(Lucas)通项。是用无理数表示有理数的范例。由于底数是无理数,计算t=12和t=24也不太方便。必须寻找另途计算。
【26】【26】就是兔子数量随着月份变化而变化的表达式,又称为Fibonacci数列的卢卡斯(Lucas)通项。是用无理数表示有理数的范例。由于底数是无理数,计算t=12和t=24也不太方便。必须寻找另途计算。
【模型求解】
【25】改写为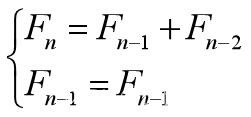 ,进一步写成向量和矩阵
,进一步写成向量和矩阵 【27】
【27】
由【27】进一步递推有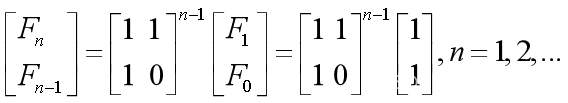 【28】
【28】
由此可以计算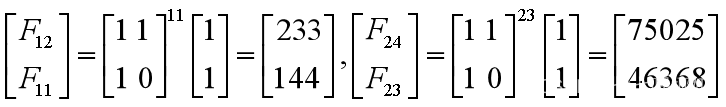



![[Qt]多线程和套接字通信](https://img-blog.csdnimg.cn/3954758e9c1e47b38eeaa11b61bec18d.png)