支持向量机是一种二分类算法，通过在高维空间中构建超平面实现对样本的分类

5. 支持向量机(非线性SVM)

---

线性可分SVM通过硬间隔最大化求出划分超平面，解决线性分类问题

线性SVM通过软间隔最大化求出划分超平面，解决线性分类问题

5.1 SVM概述

解决的问题：二分类问题

目标：通过间隔最大化策略，找一个超平面 ${\omega }^{\ast }\cdot x+b^{\ast }=0$ ，将特征空间划分为两部分 { + 1 , − 1 } \{+1,-1\} {+1,−1}

模型：定义在特征空间上的 间隔最大 的线性分类器

• 间隔最大是与感知机有区别的地方
• 通过核技巧，使SVM成为非线性分类器/回归器

策略：间隔最大化 $\to$ 凸二次化（加约束项）

• 正则化的合页损失函数最小化

算法：求解凸二次规划的最优化算法

5.1.1 分类

$$支持向量机\{\begin{array}{l}SVC(支持向量分类机)\{\begin{array}{l}线性支持向量机\{\begin{array}{l}线性可分：硬间隔最大化\\ 近似线性可分：软间隔最大化\end{array}\\ 非线性支持向量机：核技巧+软间隔最大化\end{array}\\ SVR(支持向量回归机)\end{array}$$

数据集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } , x i ∈ X ⊆ R n , y ∈ { + 1 , − 1 } , i = 1 , 2 , ⋯   , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_i\in\mathcal{X}\subseteq R^n,y\in \{+1,-1\},i=1,2,\cdots,N D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)},xi​∈X⊆Rn,y∈{+1,−1},i=1,2,⋯,N

5.2 线性可分SVM

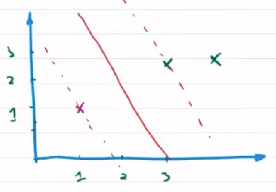
eg：SVM解决二分类问题的思路

线性可分的数据集可以简化为二维平面上的点集。

在直角坐标系中，如果有若干个点位于 $x$ 轴下方，另外若干个点位于 $x$ 轴上方，这两个点集共同构成了一个线性可分的训练数据集，而 $x$ 轴就是将它们区别开的一维超平面，也就是直线。

假设 $x$ 轴上方的点全部位于直线 $y=1$ 上及其上方，$x$ 轴下方的点全部位于直线 $y=-2$ 上及其下方。则任何平行于 $x$ 轴且在 $(-2,1)$ 之间的直线都可以将这个训练集分开。但此时面临选择哪一条直线分类效果最好的问题。

直观上看 $y=-0.5$ 最好，这条分界线正好位于两个边界中间，与两个类别的间隔 可以同时达到最大。当训练集中的数据因为噪音干扰而移动时，这个最优划分超平面的划分精确度受到的影响最小，具有很强的泛化能力

5.2.1 线性可分SVM基本思想

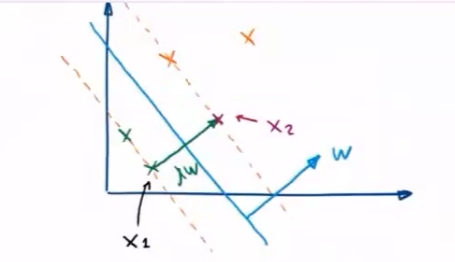
在高维的特征空间上，划分超平面可以用简单的线性方程描述
$$\omega \cdot x+b=0$$

• $n$ 维向量 $\omega$ 为法向量，决定了超平面的方向
• $b$ 为截距，决定了超平面与高维空间中原点的距离

划分超平面将特征空间分为两部分

• 法向量所指一侧——正例，$y=+1$
• 法向量反方向恻——负例，$y=-1$

决策函数：
$$f(x)=sign(\omega \cdot x+b)$$

5.2.2 策略

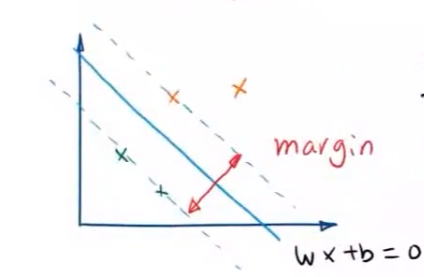
硬间隔最大化策略 ——使距离超平面最近的两个点之间的间距最大

函数间隔

超平面 $(\omega ,b)$ 关于 $(x_i,y_i)$ 的函数间隔
$${\gamma }_i=y_i(\omega \cdot x_i+b)$$

• 符号：是否分类正确
• 大小：确信程度—— $|\omega \cdot x_i+b|$ 表示点到超平面的远近程度

超平面关于数据集 $D$ 的函数间隔
$$\hat{\gamma }=\underset{x_i\in \mathcal{X}}{\min }\widehat{{\gamma }_i}=\underset{x_i\in \mathcal{X}}{\min }{y}_i(\omega \cdot +b)$$
可用函数间隔表示分类的正确性和确信程度

几何间隔

给定超平面后，特征空间中的样本点 $x_i$ 到超平面的距离可以表示为
$$\begin{gathered} +1类到超平面的距离：{\gamma }_i=\frac{\omega \cdot x_i+b}{\Vert \omega {\Vert }_2} \\ -1类到超平面的距离：{\gamma }_i=-\frac{\omega \cdot x_i+b}{\Vert \omega {\Vert }_2} \end{gathered}$$
即点被正确分类时，到超平面几何距离
$${\gamma }_i=y_i\left(\frac{\omega \cdot x_i+b}{\Vert \omega {\Vert }_2}\right)$$

• 这个距离是一个归一化距离——几何间隔

数据集 $D$ 到超平面 $(\omega ,b)$ 的几何距离
$$\begin{array}{rl}\gamma & =\underset{x_i\in \mathcal{X}}{\min }\frac{{\omega }^T\cdot x_i+b}{\Vert \omega {\Vert }_2}\\ & =\underset{x_i\in \mathcal{X}}{\min }\frac{{\hat{\gamma }}_i}{\Vert \omega {\Vert }_2}\end{array}$$

硬间隔最大化

定理 ：最大分离超平面存在且唯一
$$\{\begin{array}{l}\underset{\omega ,b}{\max }\gamma =\underset{\omega ,b}{\max }\underset{x_i\in \mathcal{X}}{\min }\frac{\omega \cdot x_i+b}{\Vert \omega {\Vert }_2}=\underset{\omega ,b}{\max }\underset{x_i\in \mathcal{X}}{\min }\frac{{\hat{\gamma }}_i}{\Vert \omega {\Vert }_2}\\ s.t.y_i\left(\frac{\omega \cdot x_i+b}{\Vert \omega \Vert }\right)\ge \gamma \end{array}$$

可通过等比例调整参数 $\omega$ 和 $b$ ，可以使每个样本到达最优划分超平面的函数距离都不小于 $1$
$$\begin{gathered} {\lambda }_i(\omega \cdot x_i+b)\ge 1,y_i=+1 \\ {\lambda }_i(\omega \cdot x_i+b)\le -1,y_i=-1 \end{gathered}$$
设 ${\lambda }_i=\frac{1}{\omega x_i+b}$ ，有
$$|{\hat{\gamma }}^{\prime }|=|\lambda \hat{\gamma }|\ge 1$$
问题变为
$$\begin{array}{rl}& \{\begin{array}{l}\underset{\omega ,b}{\max }{\gamma }^{\prime }=\underset{\omega ,b}{\max }\underset{x_i\in \mathcal{X}}{\min }\frac{\lambda y_i(\omega \cdot x_i+b)}{\Vert \lambda \omega {\Vert }_2}\ge \underset{\omega ,b}{\max }\frac{1}{\Vert {\omega }^{\prime }{\Vert }_2}\\ s.t.\frac{\lambda y_i(\omega \cdot x_i+b)}{\Vert \lambda \omega {\Vert }_2}=\frac{y_i({\omega }^{\prime }\cdot x_i+b)}{\Vert {\omega }^{\prime }{\Vert }_2}\ge {\gamma }^{\prime }\end{array}\\ \Rightarrow & \{\begin{array}{l}\underset{\omega ,b}{\max }\gamma =\underset{\omega ,b}{\max }\frac{1}{\Vert \omega {\Vert }_2}\\ s.t.y_i(\omega \cdot x_i+b)\ge 1,i=1,2,\cdots ,N\end{array}\\ \stackrel{便于凸二次规划}{⟺}& \{\begin{array}{l}\underset{\omega ,b}{\min }\frac{1}{\gamma }=\underset{\omega ,b}{\min }\frac{\Vert \omega {\Vert }_2^2}{2}\\ s.t.y_i(\omega \cdot x_i+b)-1\ge 0,i=1,2,\cdots ,N\end{array}\\ ⟺& \{\begin{array}{l}\underset{\omega ,b}{\min }\frac{\Vert \omega {\Vert }_2^2}{2}\\ s.t.1-y_i(\omega \cdot x_i+b)\le 0,i=1,2,\cdots ,N\end{array}\end{array}$$

5.2.3 原始算法

输入 ：线性可分的数据集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯   , N \begin{aligned} D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N \end{aligned} D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)},xi​∈X⊆Rn,yi​∈Y={+1,−1},i=1,2,⋯,N​
输出 ：最大分离超平面和决策函数

步骤

1. 构造并求解最优化问题
   $$\{\begin{array}{l}\underset{\omega ,b}{\min }\frac{\Vert \omega {\Vert }_2^2}{2}\\ s.t.1-y_i(\omega \cdot x_i+b)\le 0,i=1,2,\cdots ,N\end{array}$$
   凸二次规划可得最优解 ${\omega }^{\ast },b^{\ast }$

2. 可得分类超平面
   $${\omega }^{\ast }\cdot x+b^{\ast }=0$$
   决策函数 $f(x)=sign({\omega }^{\ast }\cdot x+b^{\ast })$

支持向量

在特征空间中，距离划分超平面最近的样本点能让函数间隔取等号，这些样本点称为 支持向量 ，即有点 $x_{k^{+}},x_{k^{-}}$
$$\begin{gathered} \omega \cdot x_{k^{+}}+b=1,y_{k^{+}}=+1 \\ \omega \cdot x_{k^{-}}+b=-1,y_{k^{-}}=-1 \end{gathered}$$

• $H_1,H_2$ 为分类间隔边界；$S$ 为分离超平面

两个异类支持向量到超平面的距离之和为 $\frac{2}{\Vert \omega \Vert }$ 。

因而对于线性可分的SVM任务就是：在满足上述不等式的条件下，寻找 $\frac{2}{\Vert \omega \Vert }$ 的最大值，最大化 $\frac{2}{\Vert \omega \Vert }$ 等效于最小化 $\frac{1}{2}\Vert \omega {\Vert }^2$

5.2.4 对偶形式

输入：
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } ∈ X ∈ R n , y i ∈ Y ∈ { + 1 , − 1 } , i = 1 , ⋯   , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\in \mathcal{X}\in R^n,y_i\in \mathcal{Y}\in \{+1,-1\},i=1,\cdots,N D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}∈X∈Rn,yi​∈Y∈{+1,−1},i=1,⋯,N
输出：分离超平面和决策函数

算法

1. 构造并求解对偶问题

由原始算法，可得 Lagrange 函数
$$L(\omega ,b,\alpha )=\frac{1}{2}\Vert \omega {\Vert }_2^2+\sum _{i=1}^N{\alpha }_i[1-y_i({\omega }_i\cdot x_i+b)],{\alpha }_i\ge 0$$
$\frac{1}{2}\Vert \omega {\Vert }_2^2$ 为凸函数，约束范围为凸集，则有 $局部最优解=全局最优解$
$$\begin{array}{r}最优解\in 约束域,即1-y_i({\omega }_i\cdot x_i+b)<0\\ 最优解\notin 约束域,即最优解在约束边界上，有1-y_i({\omega }_i\cdot x_i+b)=0\end{array}\}\Rightarrow \underset{{\alpha }_i}{\max }{\alpha }_i[1-y_i({\omega }_i\cdot x_i+b)]=0$$
可知 $\underset{\alpha }{\max }L(\omega ,b,\alpha )=\frac{1}{2}\Vert \omega {\Vert }_2^2$ ，即
$$\underset{\omega }{\min }\frac{1}{2}\Vert \omega {\Vert }_2^2=\underset{\omega }{\min }\underset{\alpha }{\max }L(\omega ,\alpha )$$
又由于 $\underset{\omega }{\min }\underset{\alpha }{\max }L(\omega ,b,\alpha )$ 与 $\underset{\alpha }{\max }\underset{\omega }{\min }L(\omega ,b,\alpha )$ 是对偶问题，有相同的最优解

• 对偶问题(极小中求极大)，相当于求原问题(极大中求极小)的下界

最优解满足KKT条件
$$\{\begin{array}{l}\frac{\partial L}{\partial \omega }=0\\ \frac{\partial L}{\partial b}=0\\ \frac{\partial L}{\partial {\alpha }_i}=0\\ {\alpha }_i\ge 0\\ {\alpha }_i[1-y_i({\omega }_i\cdot x_i+b)]\le 0\end{array}\Rightarrow \{\begin{array}{l}\omega -\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ -\sum _{i=1}^N{\alpha }_i{y}_i=0\\ 1-y_i({\omega }_i\cdot x_i+b)=0\\ {\alpha }_i\ge 0\\ {\alpha }_i[1-y_i({\omega }_i\cdot x_i+b)]\le 0\end{array}$$
即有 ${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$ ，代入 $L(\omega ,b,\alpha )$

$$\begin{array}{rl}\underset{\omega ,b}{\min }L(\alpha )& =\frac{1}{2}({\omega }^{\ast }{)}^T{\omega }^{\ast }+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i{\omega }^{\ast }\cdot x_i-\sum _{i=1}^N{\alpha }_i{y}_{i}b\\ & =\frac{1}{2}\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\sum _{i=1}^N{\alpha }_i{y}_i{x}_i+\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{y}_i\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\\ & \stackrel{x_j\cdot ,x_i为向量点积，其余部分为标量}{=}\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^N{\alpha }_i\\ & =\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j\end{array}$$
对偶问题
$$\{\begin{array}{l}\underset{\alpha }{\max }L(\alpha )=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j\\ s.t.{\alpha }_i\ge 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$
求解对偶问题，可得 ${\alpha }^{\ast }=\left(\begin{array}{r}{\alpha }_1^{\ast }\\ {\alpha }_2^{\ast }\\ ⋮\\ {\alpha }_N^{\ast }\end{array}\right)$

2. 计算参数

由 ${\alpha }^{\ast }$ 可得 ${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$

• 结论：对于支持向量，有 ${\alpha }_j^{\ast }>0$ ，其余点 ${\alpha }^{\ast }=0$

间隔边界上的点，满足
$$\begin{array}{rl}& y(\omega \cdot x+b)=1\\ & y^2(\omega \cdot x+b)=y\\ \Rightarrow & \omega \cdot x+b=y\end{array}$$
将 ${\omega }^{\ast }$ 代入支持向量
$$\begin{array}{rl}& {\omega }^{\ast }{x}_j+b^{\ast }=y_j\\ \Rightarrow & b^{\ast }=y_j-{\omega }^{\ast }{x}_j=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)\end{array}$$

3. 求得分离超平面

$$\{\begin{array}{l}{\omega }^{\ast }x+b^{\ast }=0\\ 分类决策函数f(x)=sign({\omega }^{\ast }x+b)\end{array}\Rightarrow \{\begin{array}{l}\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\cdot x+\left(y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)\right)=0\\ f(x)=sign\left(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\cdot x+y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)\right)\end{array}$$

优点

• 对偶问题易于求解
• 引入核函数，推广到非线性分类问题

例题

有样本 $+1:x_1=(3,3),x_2=(4,3)$ ，$-1:x_3=(1,1)$

由对偶算法
$$\{\begin{array}{l}\underset{\alpha }{\min }\left(\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N{\alpha }_i\right)\\ s.t.{\alpha }_i\ge 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0,i=1,2,\cdots ,N\end{array}$$
代入后有
$$\{\begin{array}{l}\begin{array}{c}\underset{\alpha }{\min }L(\alpha )=\frac{1}{2}(18{\alpha }_1^2+25{\alpha }_2^2+2{\alpha }_3^2+42{\alpha }_1{\alpha }_2-12{\alpha }_1{\alpha }_3-14{\alpha }_2{\alpha }_3)-({\alpha }_1+{\alpha }_2+{\alpha }_3)\end{array}\text{\hspace{1em}(1)}\\ s.t.{\alpha }_1+{\alpha }_2-{\alpha }_3=0\\ {\alpha }_i\ge 0\end{array}$$
将 ${\alpha }_3={\alpha }_1+{\alpha }_2$ 代入 $(1)$
$$S({\alpha }_1,{\alpha }_2)=4{\alpha }_1^2+\frac{13}{2}{\alpha }_2^2+10{\alpha }_1{\alpha }_2-2{\alpha }_1-2{\alpha }_2$$
令 $\frac{\partial S}{\partial {\alpha }_1}=0$ ，$\frac{\partial S}{\partial {\alpha }_2}=0$ 可得 $({\alpha }_1,{\alpha }_2{)}^T=(\frac{3}{2},-1{)}^T$ ，但不满足约束条件

可知最优解在约束边界上
$$\begin{gathered} 若{\alpha }_1=0，令\frac{\partial S}{\partial {\alpha }_2}=0\Rightarrow {\alpha }_2=\frac{2}{13}\Rightarrow S(0,\frac{2}{13})=-\frac{2}{13} \\ {\alpha }_2=0，令\frac{\partial S}{\partial {\alpha }_1}=0\Rightarrow {\alpha }_1=\frac{1}{4}\Rightarrow S(\frac{1}{4},0)=-\frac{1}{4} \end{gathered}$$
$\therefore$ $S({\alpha }_1,{\alpha }_2)$ 在 $(\frac{1}{4},0{)}^T$ 上取最小，${\alpha }_3={\alpha }_1+{\alpha }_2=\frac{1}{4}$

由于 ${\alpha }_1={\alpha }_3=\frac{1}{4}\ne 0$ ，故 $x_1,x_3$ 为支持向量
$$\begin{array}{rl}{\omega }^{\ast }& ={\alpha }_1{y}_1{x}_1+{\alpha }_3{y}_3{x}_3\\ & =\frac{1}{4}\left(\begin{array}{r}3\\ 3\end{array}\right)+\frac{1}{4}(-1)\left(\begin{array}{r}1\\ 1\end{array}\right)=\left(\begin{array}{r}\frac{1}{2}\\ \frac{1}{2}\end{array}\right)\\ b^{\ast }& =y_3-\sum _{i=1}^3{\alpha }_i{y}_i(x_i\cdot x_3)=-2\end{array}$$
所以有分离超平面 $\frac{1}{2}{x}^{(1)}+\frac{1}{2}{x}^{(2)}-2=0$ ，决策函数 $f(x)=sign(\frac{1}{2}{x}^{(1)}+\frac{1}{2}{x}^{(2)}-2)$