1、原地移除数组中所有的元素val,要求时间复杂度为O(N),空间复杂度为O(1)。
OJ链接:27. 移除元素 - 力扣(LeetCode)
分析:
法1:挪到数据,思路如顺序表的头删,将后面的数据向前挪动将其覆盖即删除成功。时间复杂度——做最坏的打算,如果数组所有元素都等于val,则时间复杂度为O(N^2),不符合要求。
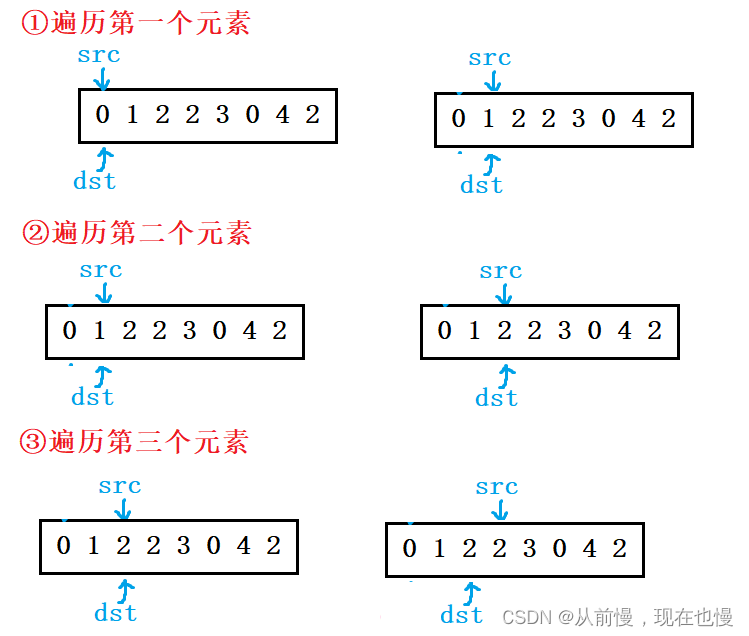
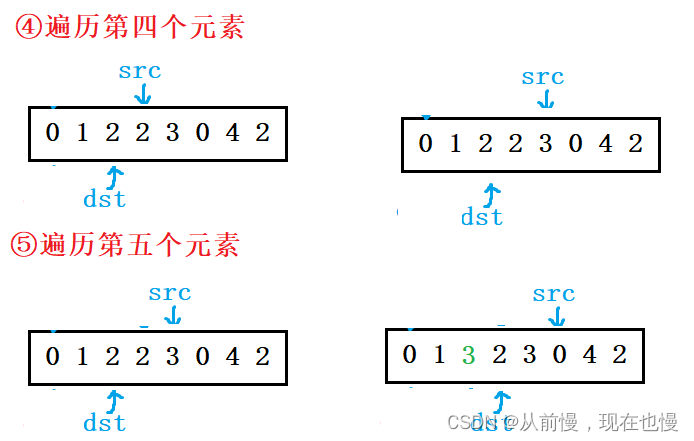
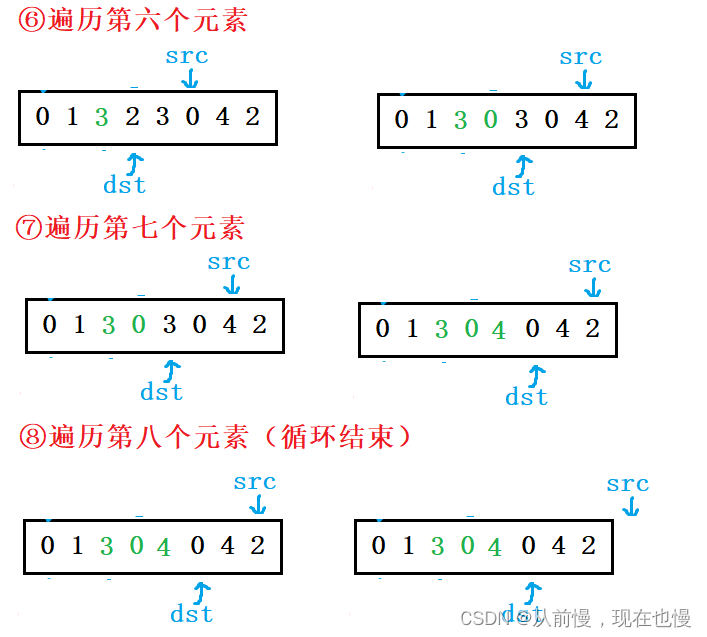
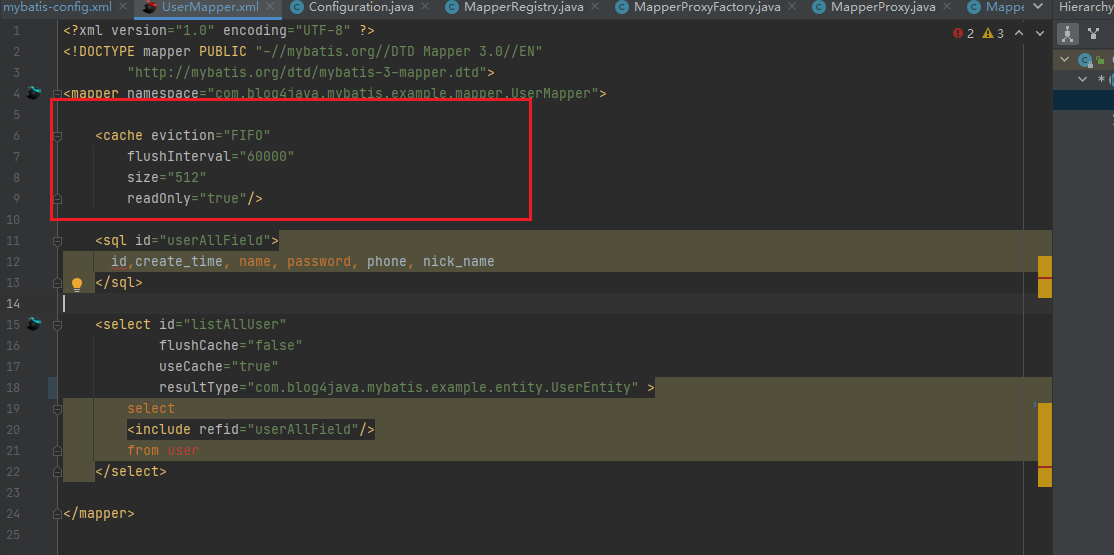
法2:创建一块额外的空间dst,将原数组中不等于val的值拷贝到dst中,再将dst拷贝回原数组即可。图示:
但是该法的空间复杂度为O(N),不符合要求。
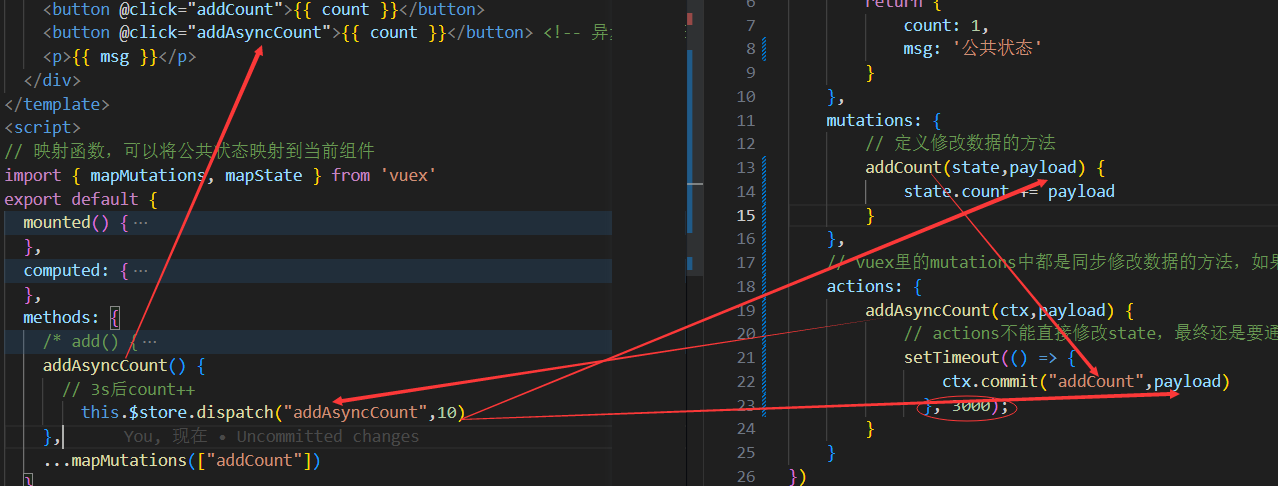
法3:法2空间复杂度不符合要求,那我们能不能就在原数组上挪动数据呢?当然是有的,这就双指针法(双下标)——创建两个指针(下标)src,dst指向原数组,src遍历原数组,如果nums[src] != val,则nums[dst++] = nums[src];如果nums[src] == val,则src++。图示:
法3代码演示:
int removeElement(int* nums, int numsSize, int val)
{
int src = 0;
int dst = 0;
while(src < numsSize)
{
if(nums[src] != val)
{
nums[dst++] = nums[src++];
}
else
{
src++;
}
}
return dst;
}2、删除排序数组中的重复项。
OJ链接:26. 删除有序数组中的重复项 - 力扣(LeetCode)
要求:时间复杂度0(N),空间复杂度O(1)
分析:
①删除有序数组中的重复项,返回删除后的数组新长度,也叫去重算法。
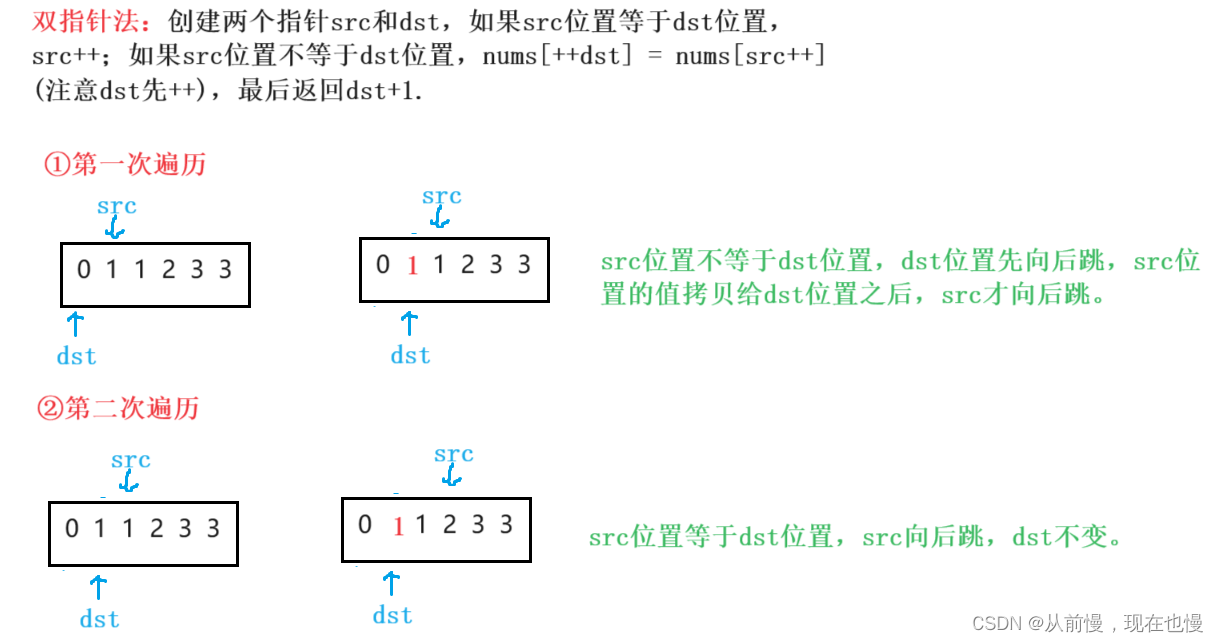
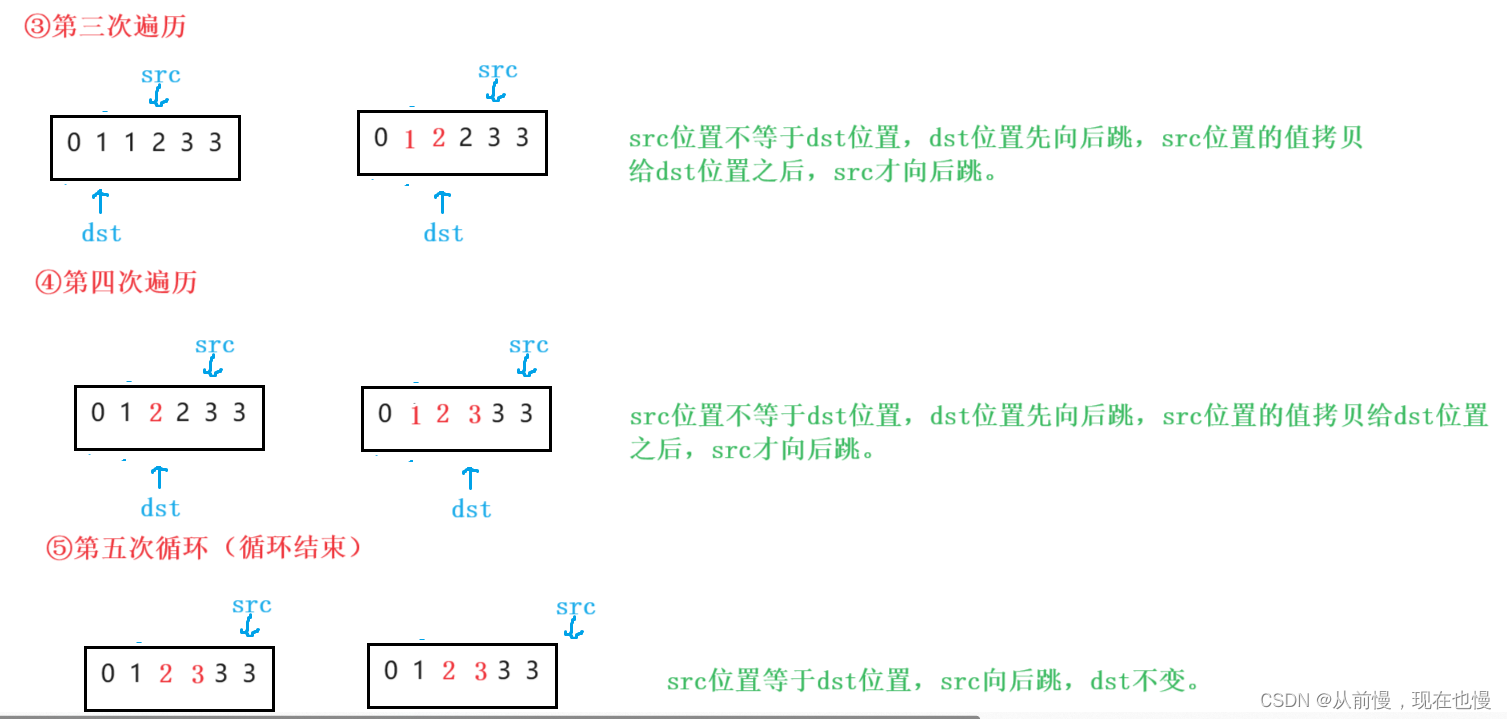
②思路依旧使用双指针法:只是有了一些变化。创建两个伪指针(即定义两个下标变量),分别为src开始指向数组的第二个元素,dst开始指向数组的第一个元素;src遍历数组,每一次遍历时都要判断src位置是否等于dst位置,相等则将src位置的值拷贝到dst位置,同时dst位置向后+1。最后返回dst+1即可(一位dst开始时指向的数组的第一个元素,数组的下标从0开始,所以最后返回时要+1)。图示:
相当于src指针遍历数组,dst指针存储数组去重之后的新数据。
代码演示:
int removeDuplicates(int* nums, int numsSize)
{
//定义两个下标变量
int src = 1;
int dst = 0;
//去重
while(src < numsSize)
{
if(nums[src] == nums[dst])
{
src++;
}
else
{
nums[++dst] = nums[src++];
}
}
//注意数组的下标从0开始,所以dst+1
return dst + 1;
}3、合并两个有序数组。
OJ链接:88. 合并两个有序数组 - 力扣(LeetCode)
分析:
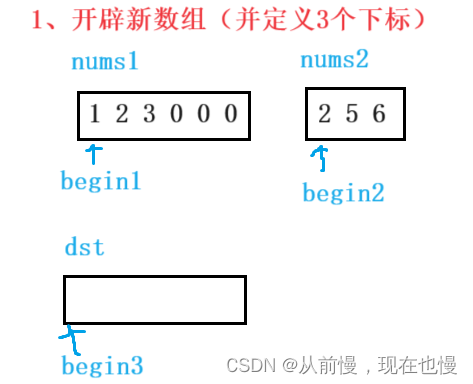
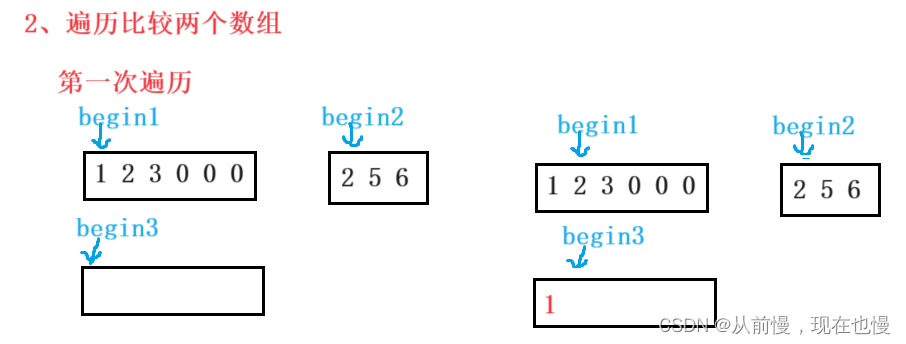
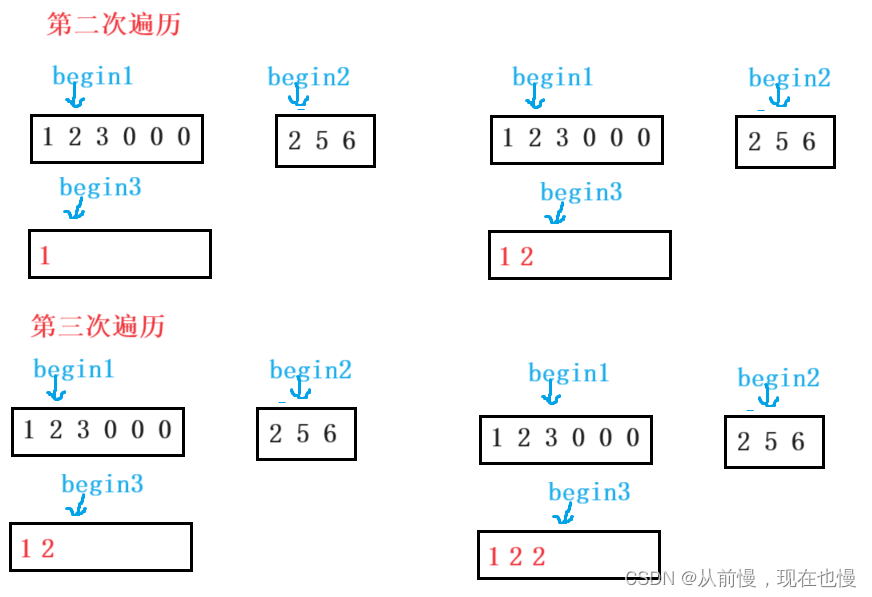
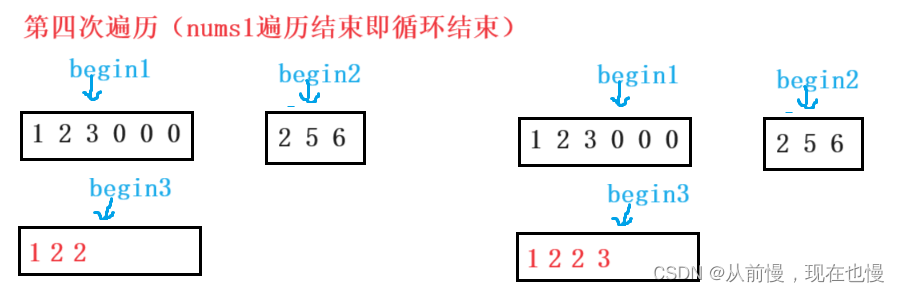
法1:开辟额外的空间:①开辟新数组大小为m+n;②遍历比较两个数组(循环条件:有一个数组遍历结束即循环结束)。如果nums1[begin1] < nums2[begin2],则先将begin1位置的值拷贝到新数组;否则先将begin2位置的值拷贝到新数组,再begin2++。③将剩余的数组直接拷贝到新数组后面;④最后将新数组拷贝回nums1即可。图示:
时间复杂度O(M+N),空间复杂度O(M+N)。
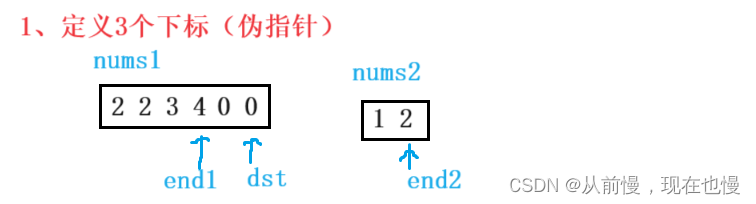
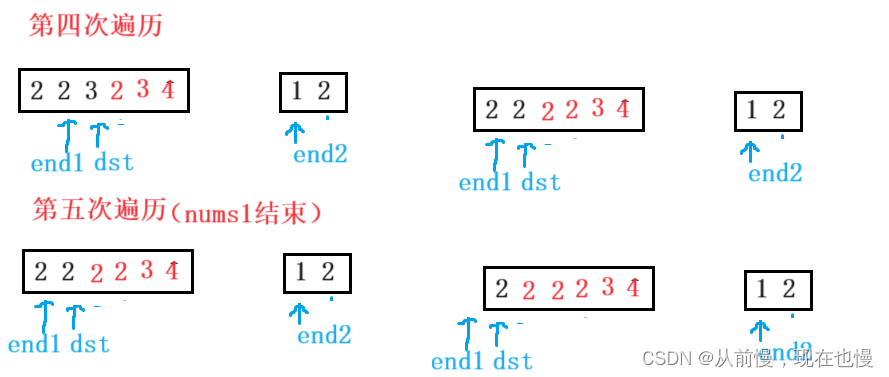
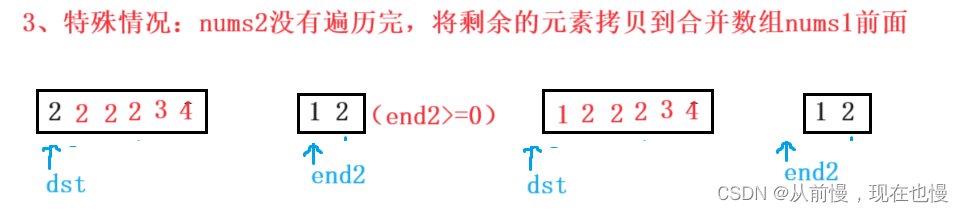
法2:原地合并数组:①定义三个下标(伪指针):end1指向nums1有效数据的最后一个;end2指向nums有效数据的最后一个;dst指向合并数组nums1的最后一个;②逆向双指针:end1和end2两个指针从后向前遍历比较两个数组(为什么不从前往后遍历呢?因为从前遍历,每一次插入都要向后挪动数据),有一个数组遍历结束循环即停止。如果nums1[end1]>nums2[end2],则nums1[dst--]=nums1[end1--];否则nums1[dst--]=nums2[end2--]。③特殊情况:如果是nums2没有遍历结束,则需继续将nums2剩余的元素依次拷贝到nums1前面。图示:
时间复杂度:O(M+N);空间复杂度O(1).
法1:开辟额外的空间代码演示:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
//开辟新数组大小m+n
int dst[m + n];
//分别定义三个数组下标变量
int begin1 = 0;
int begin2 = 0;
int begin3 = 0;
//先遍历比较两数组(循环条件:有一个数组遍历结束即循环结束)
//如果nums1[begin1]<nums2[begin2],则先将begin1位置的值拷贝到新数组,再begin1++
//否则先将begin2位置的值拷贝到新数组,再begin2++
while(begin1 < m && begin2 < n)
{
if(nums1[begin1] < nums2[begin2])
{
dst[begin3++] = nums1[begin1++];
}
else
{
dst[begin3++] = nums2[begin2++];
}
}
//将剩余的数组直接拷贝到新数组后面
if(begin1 < m)
{
memmove(dst + begin3,nums1 + begin1,(m - begin1)*sizeof(int));
}
else if(begin2 < n)
{
memmove(dst + begin3,nums2 + begin2,(n - begin2)*sizeof(int));
}
//最后将新数组拷贝回nums1即可
memmove(nums1,dst,(m + n)*sizeof(int));
}法2:原地合并数组代码演示:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
//定义三个下标
int end1 = m - 1;//指向nums1有效数据的最后一个
int end2 = n - 1;//指向nums2数据的最后一个
int dst = m + n -1;//指向合并数组nums1的最后一个
//逆向双指针合并:end1和end2两个指针从后往前遍历两个数组,有一个数组遍历结束即停止。
while(end1 >= 0 && end2 >=0)
{
if(nums1[end1] > nums2[end2])
{
nums1[dst--] = nums1[end1--];
}
else
{
nums1[dst--] = nums2[end2--];
}
}
//特殊情况:如果nums2没有遍历完,则需将nums2前面的元素拷贝到nums1中
while(end2 >= 0)
{
nums1[dst--] = nums2[end2--];
}
}