螺旋折线

前言

在写完题目查看题解的时候，被acwing大佬的思路所震撼，所以按照自己的理解将
大佬的思路复刻一遍展现给大家，同时丰富了内容，使得 0基础的小伙伴都能够看懂，此外还给出了自己的代码为大家当反面教材，喜欢的小伙伴可以点个关注啦！

题目描述

如下图所示的螺旋折线经过平面上所有整点恰好一次。

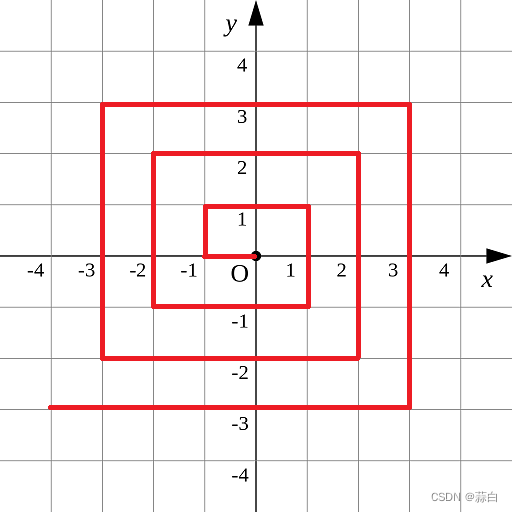
对于整点 (X,Y)，我们定义它到原点的距离 dis(X,Y) 是从原点到 (X,Y) 的螺旋折线段的长度。

例如 dis(0,1)=3,dis(−2,−1)=9

给出整点坐标 (X,Y)，你能计算出 dis(X,Y) 吗？

输入格式
包含两个整数 X,Y。

输出格式
输出一个整数，表示 dis(X,Y)。

数据范围
−109≤X,Y≤109
输入样例：
0 1
输出样例：
3

题目分析

优化思路

很明显，图形的构造是有规律的，站在编程的角度去审视，我们如何将整个图形划分为有规律的小块呢？
我们发现每一圈的许多点横纵坐标绝对值的最大值是相同的，我们依据此特点将这些点划分成一层，看图

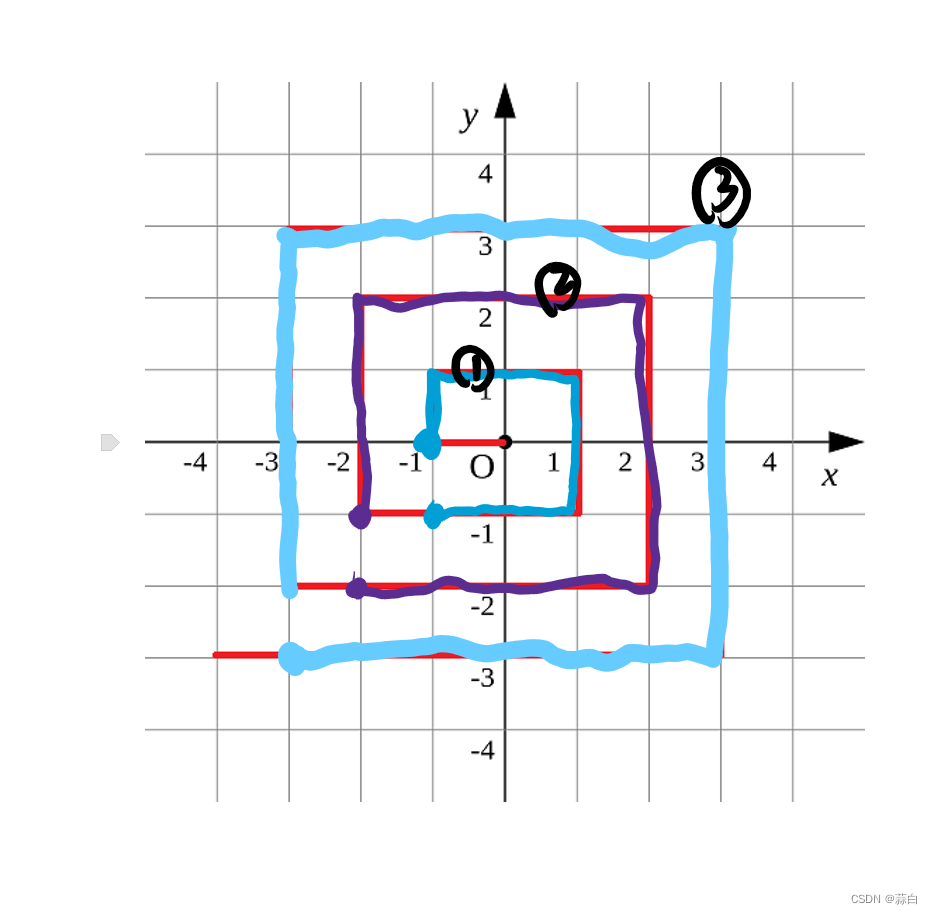
现在我们分好层了，那么对于每一层而言，我们还要进行分析，那么怎么划分每一层使得我们的分析思路最简单呢？
从对称性入手，通过这样的手段使得每一层分化为近乎完整的两个部分

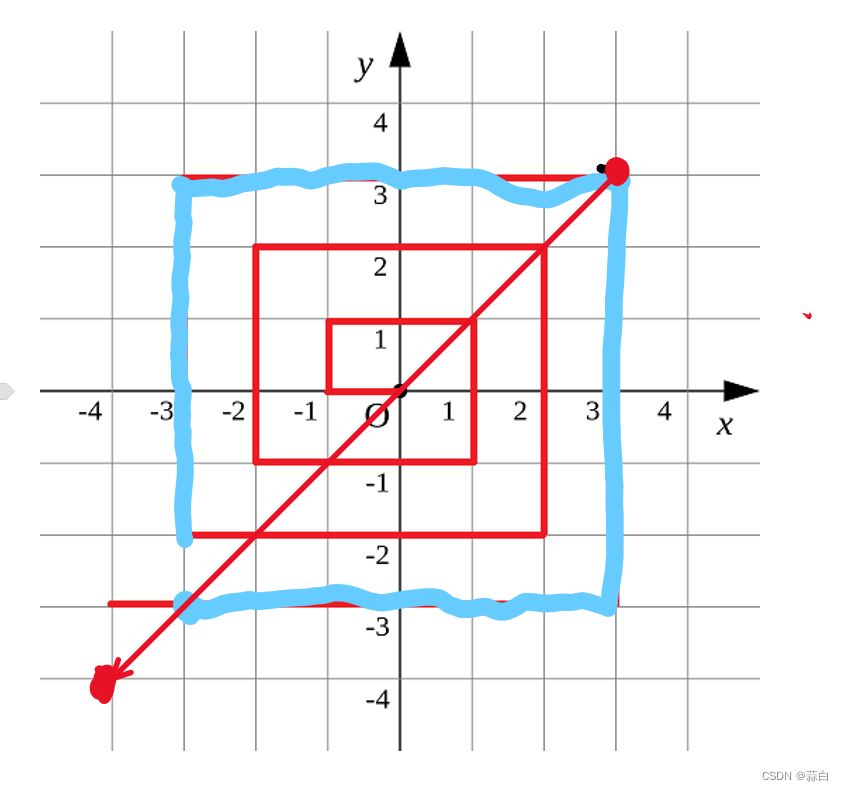
然后我们对关键的对称点分析，发现有：

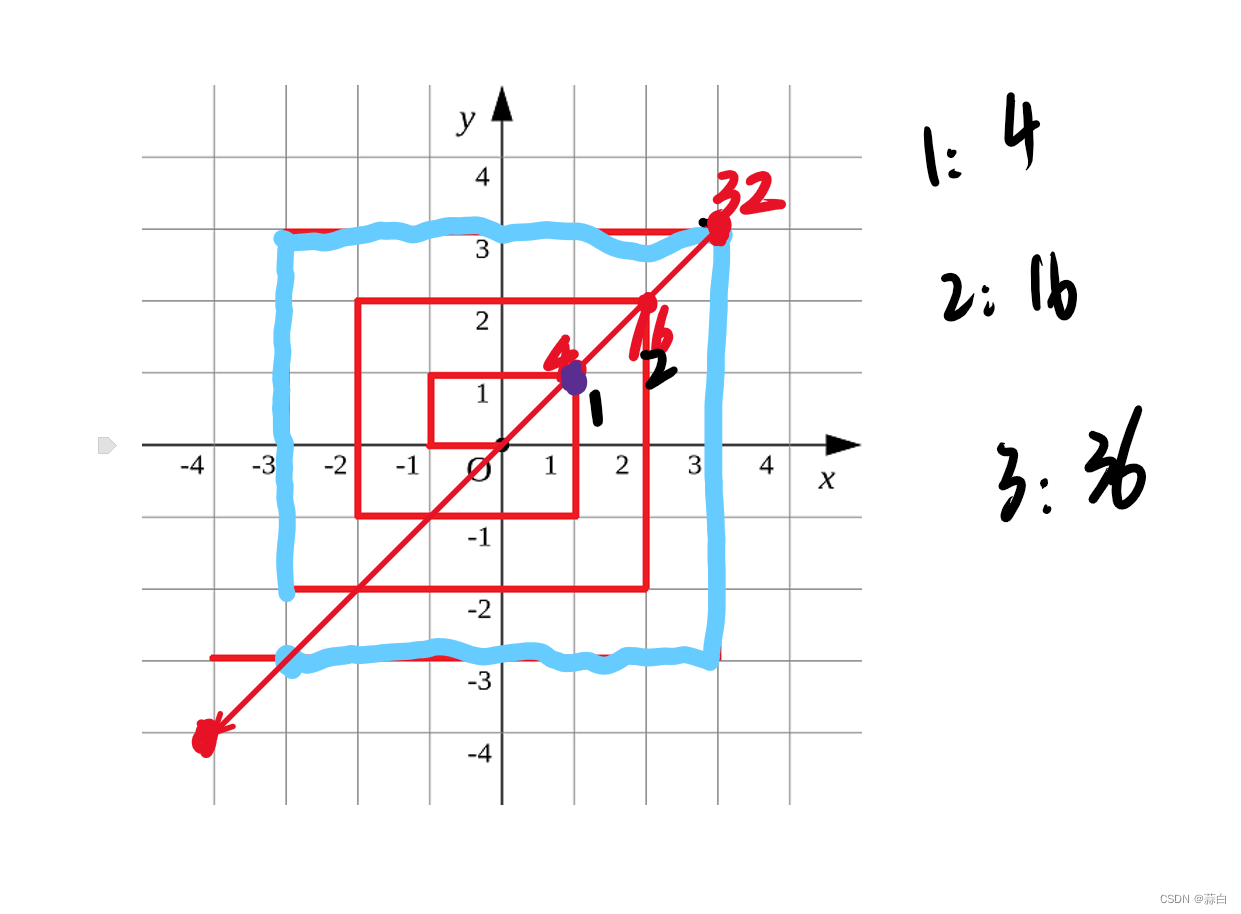
发现规律：4 * n^2
对于对称点的左边那些目标点，那些点的长度为 4 * n^2 –（对称点到目标点的曼哈顿距离）
对于对待点的右边那些目标点，那些点的长度为 4 * n^2 +（对称点到目标点的曼哈顿距离)

知识点补充【曼哈顿距离】

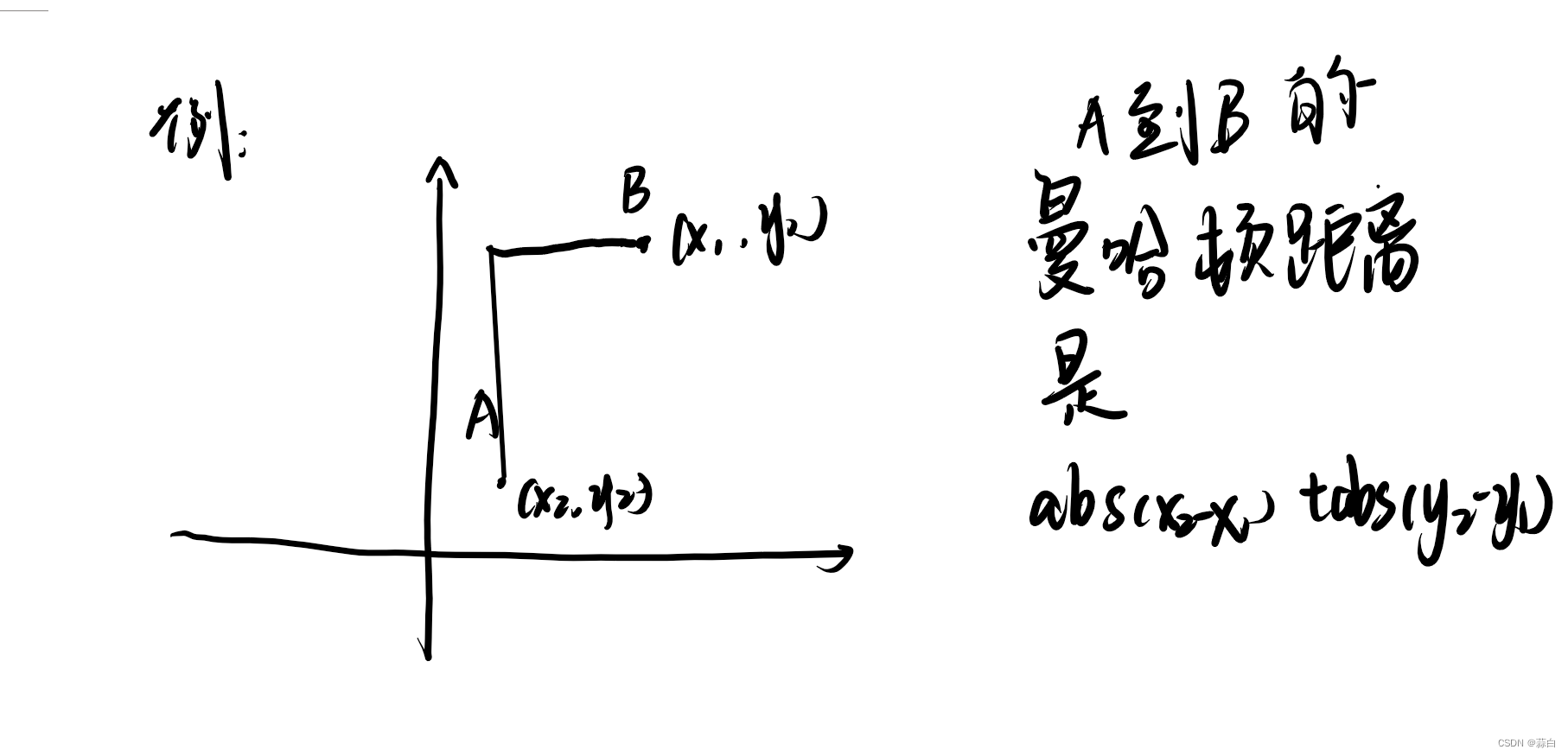
假设有两个点A(x1, y1)和B(x2, y2)，则它们之间的曼哈顿距离可以用以下公式表示：

d = |x1 - x2| + |y1 - y2|

曼哈顿距离的名称源自纽约曼哈顿区的街道布局，因为在曼哈顿区，两点之间的最短路径是沿着网格状的街道行走，而不是直线距离。

曼哈顿距离在计算机科学和数据分析中经常被使用，特别是在图像处理、路线规划和聚类分析等领域。它的优点之一是计算简单快速，而且对于在坐标系中移动的物体来说更加直观。

代码

#include<iostream>
#include<cmath>
using namespace std;
typedef long long LL;//由于累加的数据过大，这里用
// long long 来进行存储
int main(){
    LL x,y;
    cin>>x>>y;
    LL n=max(abs(x),abs(y));
    if(y<=x){//这里判断是右边的部分
        cout<<4*n*n+abs(x-n)+abs(y-n)<<endl;
    }
    else{
        cout<<4*n*n-abs(x-n)-abs(y-n)<<endl;
    }
}

未优化思路【笨方法】

这里对每一层的划分是如下图所示：

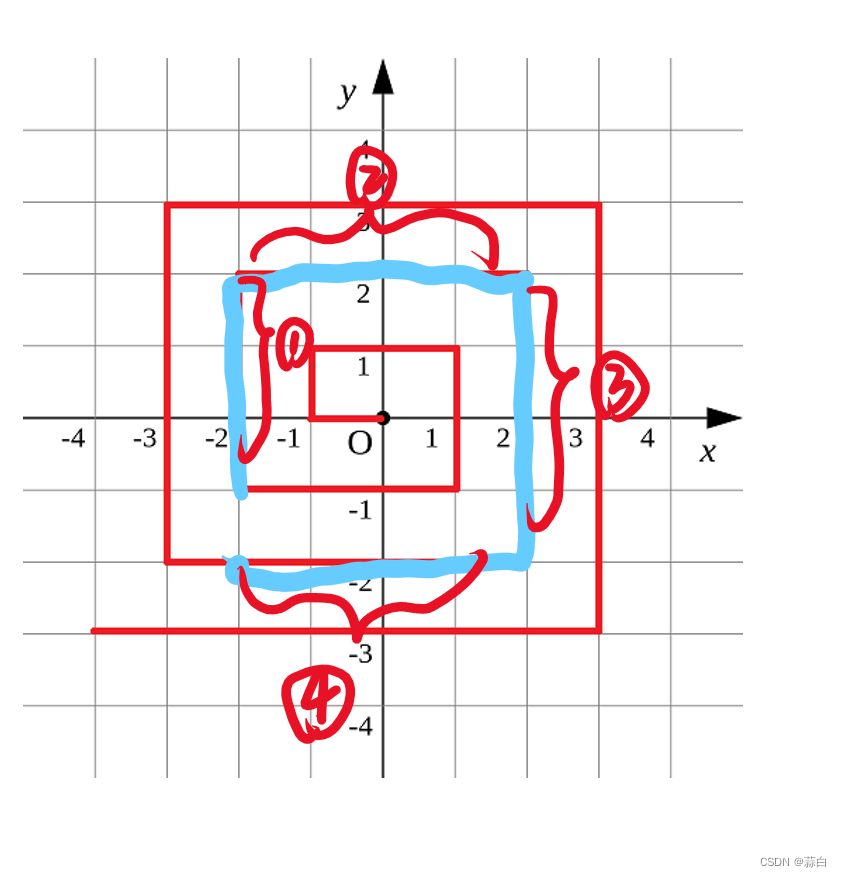
只能对 9 / 15 个数据

#include<iostream>
#include<cmath>
using namespace std;
typedef long long LL;
int main(){
    int x,y;
    cin>>x>>y;
    LL res=0;
    int flag=0;
    if(x==0 && y==0){
        res=0;
    }
    else{
        
        flag=max(abs(x),abs(y));
        // cout<<abs(x)<<' '<<abs(y)<<endl;
        
        if(x==-flag && y>=-flag+1 && y<flag){
            res+=abs(x+flag)+abs(y+flag-1);
        }
        else if(y==flag && x>-flag && x<=flag){
            res+=abs(x+flag)+abs(y+flag-1);
        }
        else if(x==flag && y<flag && y>=-flag) res+=4*flag-1+flag-y;
        else if(y== -flag && x<flag && x>=-flag) res+=flag-x + 6*flag-1;
    }
    if(flag){
        for(int i=flag-1;i>=1;i--){
            res+=8*i-1;
        }
    }
    cout<<res+flag<<endl;
    
}