一:引入
1.优先队列:大家还记得我们上节课讲的赫夫曼树,我使用了一个优先队列大大减轻了我们的开发任务,但是大家知道这个优先队列内部是如何实现的呢?
解决: 大顶堆,优先删除堆顶
2.如何实现一个用户热门搜索排行榜功能(微博热搜)?给你一个包含1亿关键词的用户检索的日志,如何取出排行前10的关键词。 给你的处理机器:2CPU 2G内存 一台。年龄,0~200
解决: 1.统计出现的频率 2.维护一个大小为10的大顶堆
3.2.TOP K问题,比如给你一串1000万的数字 求前k大的数。 一种是静态的数据 一种是动态的的数据
二:堆的定义
堆是什么?堆是一种特殊的树,他需要满足以下两点:
1.是一颗完全二叉树(除了最后一层,其他层每个节点都是满的且最后一层的节点都要靠左排列。)
2.其每一个节点的值都大于等于或者小于等于其左右子节点的值。
但是和二叉搜索树不同: 左节点小于根节点,右节点大于根节点
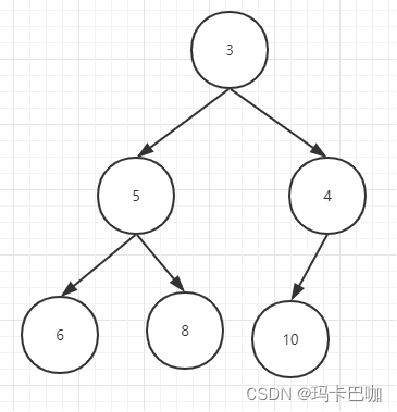
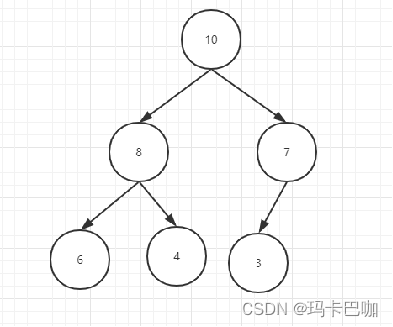
小顶堆 
大顶堆
三:堆的操作
3.1 堆的存储
如果大家还记得我之前讲的,那肯定都很清楚完全二叉树的最佳存储结构就是数组。因为它有着特殊的属性,直接利用下标就可以表示左右节点
比如右边的结构:
1:10
2:8
3:7
4:6
5:4
6:3
还记得我之前讲的那个左右子节点的公式吧: 左=2*I i就是我们当前点所在数组的下标。 右=2*i+1
如果下标从0开始开始 ,这两个公式:2*i+1,2*i+2
3.2 堆的插入(两种插入方式:从上往下,从下往上)
堆插入的位置就叫堆化
从上往下:其实就是把插入的点放到堆顶,然后依次往下比较即可。
从下往上:加入我们在右图插入9,很显然此时插入9后我们是不满足堆树的性质的,那怎么办呢? 其实只要做下交换就可以了,直到依次往上做到不能交换为止,看下图。
完全二叉树。类似于满二叉树,32层就可以21亿+个点,n个数交换多少 次?
顶多交换次数就是书的高度,又因为最后一层不用管,所以最多交换Logn-1次
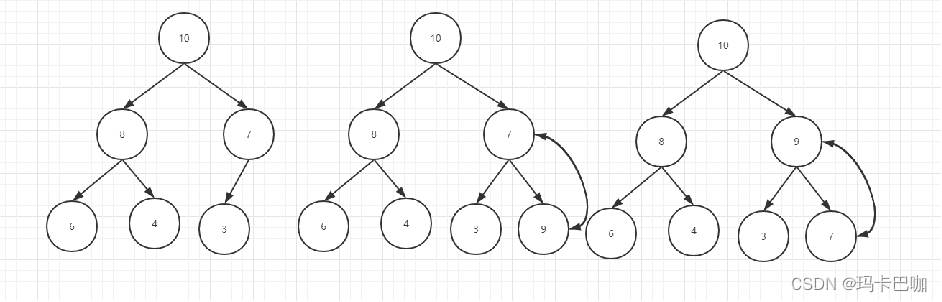
9插入过程
3.3 堆的删除
1.删除堆顶: 就把堆顶的数与最后一个做交换,然后再堆排序,最终还能保证是一课完全二叉树,否则会少结点。
四:堆树应用
1.堆排序
大家还记得我之前讲排序的时候我们还有一个堆排序没讲,今天我们来看看,如果利用这个堆树进行排序呢?
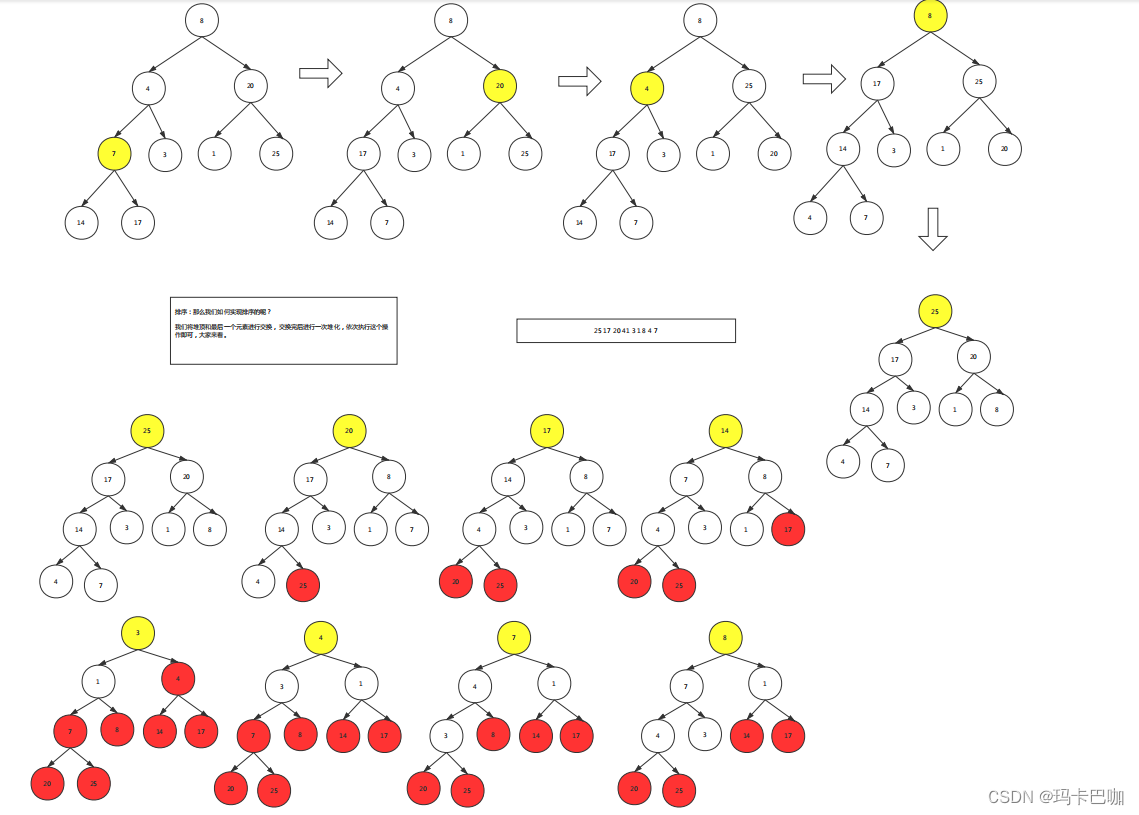
假设给你一个序列: 8 4 20 7 3 1 25 14 17
利用堆树进行排序:
1.先按照序列顺序存储在完全二叉树中。
建堆:
2.从最后一个非叶子节点堆化。为什么是最后一个非叶子节点而不是最后一个叶子节点呢? 看例子:
一种:从无到右,就是从头往后建
二种:修正,从后往前。从数组的后面往前走
排序:那么我们如何实现排序的呢?我们将堆顶和最后一个元素进行交换,交换完后进行一次堆化,依次执行这个操作即可,大家来看。同时每次排完序后已经排好的就不需要再次排序了。
package tree.堆树;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int data[] = { 8, 4, 20, 7, 3, 1, 25, 14, 17 };
heapSort(data);
System.out.println(Arrays.toString(data));
}
/**
* 有int start, int end:参数是因为已经建好的就不需要再比较了,所以每次都有范围
* @param data
* @param start
* @param end
*/
public static void maxHeap(int data[], int start, int end) { // 建一个大顶堆,end表示最多建到的点 lgn
int parent = start;
int son = parent * 2 + 1; // 下标是从0开始的就要加1,从1就不用
while (son < end) {
int temp = son;
// 比较左右节点和父节点的大小 son:表示左结点 son+1:表示右结点
if (son + 1 < end && data[son] < data[son + 1]) { // 表示右节点比左节点到
temp = son + 1; // 就要换右节点跟父节点
}
// temp表示的是 我们左右节点大的那一个
if (data[parent] > data[temp])
return; // 不用交换
else { // 交换
int t = data[parent];
data[parent] = data[temp];
data[temp] = t;
parent = temp; // 继续堆化
son = parent * 2 + 1;
}
}
return;
}
public static void heapSort(int data[]) {
int len = data.length;
for (int i = len / 2 - 1; i >= 0; i--) { //o(nlgn) len / 2 - 1:代表最后一个非叶子结点开始
maxHeap(data, i, len); //
}
for (int i = len - 1; i > 0; i--) { //o(nlgn)
int temp = data[0];
data[0] = data[i];
data[i] = temp;
maxHeap(data, 0, i); //这个i能不能理解?因为len~i已经排好序了
}
}
}