A.Make It Zero

思维题

当n为偶数时,对1到n异或使得1到n全部变成一样的数,再对1到n异或,使得全部变成0

当n为奇数时,对1到2异或使得1到2全部变成一样的,再对1到2异或,使得1到2都变成0,然后再两次对2到n

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
//#define int long long
using namespace std;
const int N=110;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=1; i<=n; i++) {
        cin>>a[i];
    }
    if(n%2==0) {
        cout<<2<<endl;
        cout<<1<<' '<<n<<endl;
        cout<<1<<' '<<n<<endl;
    }
    else{
        cout<<4<<endl;
        cout<<1<<' '<<2<<endl;
        cout<<1<<' '<<2<<endl;
        cout<<2<<' '<<n<<endl;
        cout<<2<<' '<<n<<endl;
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

B.2D Traveling

分三种情况,当起始点都为主要城市,为0,当起始点其中一个为主要城市,就找主要城市中离另一个起始点距离最近,并和起始点本身两点线段距离取min,当起始点都不是主要城市,就找离起点最近的主要城市和离终点最近的主要城市,然后两者距离加起来,和起始点本身两点线段距离取min

当时问题出在第三种情况想错了,想的是在起始点形成的矩形里面找离起点最近的主要城市和离终点最近的主要城市,然后两者距离加起来,和起始点本身两点线段距离取min,实际上错的离谱了

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int xx[N],yy[N];
int n,k,a,b;
void solve() {
    cin>>n>>k>>a>>b;
    int min1=4e9,min2=4e9;
    int min1x,min1y,min2x,min2y;
    for(int i=1; i<=n; i++) cin>>xx[i]>>yy[i];
    int x1=xx[a],y1=yy[a],x2=xx[b],y2=yy[b];
    int d=abs(x1-x2)+abs(y1-y2);
    if(a<=k&&b<=k) {
        cout<<0<<endl;
        return;
    }
    if(a<=k||b<=k) {
        if(a<=k) {
            for(int i=1; i<=k; i++) {
                int dist=abs(xx[i]-xx[b])+abs(yy[i]-yy[b]);
                d=min(d,dist);
            }
            cout<<d<<endl;
            return;
        } else {
            for(int i=1; i<=k; i++) {
                int dist=abs(xx[i]-xx[a])+abs(yy[i]-yy[a]);
                d=min(d,dist);
            }
            cout<<d<<endl;
            return;
        }
    }
//    bool ok=false;
//    for(int i=1; i<=k; i++) {
//        if(xx[i]<min(x1,x2)||xx[i]>max(x1,x2)||yy[i]<min(y1,y2)||yy[i]>max(y1,y2)) continue;
//        ok=true;
//        int d1=abs(xx[i]-x1)+abs(yy[i]-y1);
//        int d2=abs(xx[i]-x2)+abs(yy[i]-y2);
//        if(min1>d1) min1=d1;
//        if(min2>d2) min2=d2;
//    }
//    if(ok) d=min(d,min1+min2);
//    cout<<d<<endl;
    for(int i=1; i<=k; i++) {
        int d1=abs(xx[i]-x1)+abs(yy[i]-y1);
        int d2=abs(xx[i]-x2)+abs(yy[i]-y2);
        if(min1>d1) min1=d1;
        if(min2>d2) min2=d2;
    }
    d=min(d,min1+min2);
    cout<<d<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

C.Fill in the Matrix

构造题

我们第一行构造为0,1,...m-1

然后第二行为1,2,...m-1,0

依次循环右移

循环右移x次能得到x+1

我们如果循环n次,则能得到n+1,如果循环右移m-1次,则能得到m

我们取min(n+1,m)

如果循环右移了m次,那么每列都得到m,所以我们最多循环右移m-1次,然后如果n小于m-1的话,那么连m-1次都移不了

最后剩下的行就全部补成之前的数就行了,补成1,2,...m-1,0

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<set>
#define endl '\n'
#define int long long
using namespace std;
int n,m;
void solve() {
    cin>>n>>m;
    if(m==1) cout<<0<<endl;
    else cout<<min(m,n+1)<<endl;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i<=m-1) cout<<((i+j-1)%m+m)%m<<' ';
            else cout<<(j%m+m)%m<<' ';
        }
        cout<<endl;
    }
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

D1.Candy Party (Easy Version)

this version everyone must give candies to exactly one person and receive candies from exactly one person.每个人都必须分出去一个2的幂次,也必须接收一个2的幂次,也就是减一个2的次幂,加一个2的幂次

有一个结论:任何一个数分解成两个2的幂次的形式是唯一的

如图:

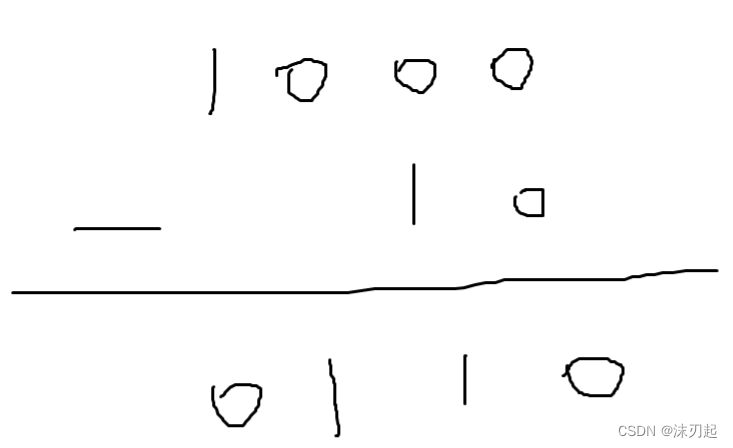
一个数n分解成两个二次幂的差,小的那个1的位置和n的最低位的1同,大的那个1的位置比n的最高位的1的位高1

但是不一定所有的n都可以分解成功,要求是它的二进制表示中1是连续的

由于总数一定,所以平均数一定,那么对于每个数都是一个2的次幂出去,一个2的次幂进来,最后统计是否减去的2的次幂和加上的2的次幂是否相同

注意,每次都要初始化

 AC代码:

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
bool check(int n){
    if(n>0&&(n&(n-1))==0) return true;
    return false;
}
int lowbit(int x){
    return x & (-x);
}
void solve() {
    cin>>n;
    int sum=0;
    vector<int> bit(31, 0);//bit每次要初始化
    for(int i=1;i<=n;i++) {
        cin>>a[i];
        sum+=a[i];
    }
    if(sum%n){
        cout<<"No"<<endl;
        return;
    }
    int d=sum/n;
    for(int i=1;i<=n;i++){
        if(a[i]==d) continue;
        int diff=abs(a[i]-d);
        int p=lowbit(diff);//小
        int q=diff+p;//大
        if(!check(q)){
            cout<<"No"<<endl;
            return;
        }
        //接受大的,减去小的
        if(a[i]<d){
            bit[log2(q)]++;
            bit[log2(p)]--;
        }
        //接受小的,减去大的
        else{
            bit[log2(p)]++;
            bit[log2(q)]--;
        }
    }
    for(int i=0;i<31;i++){
        if(bit[i]){
            cout<<"No"<<endl;
            return;
        }
    }
    cout<<"Yes"<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}