1.让N个人过河所需最少船​编辑

2.最长回文子序列

3.最少添加字符让字符串变回文串​编辑

4.回文子串的最少切割次数

5.移除字符使字符串变回文串的方案数​编辑

---

1.让N个人过河所需最少船

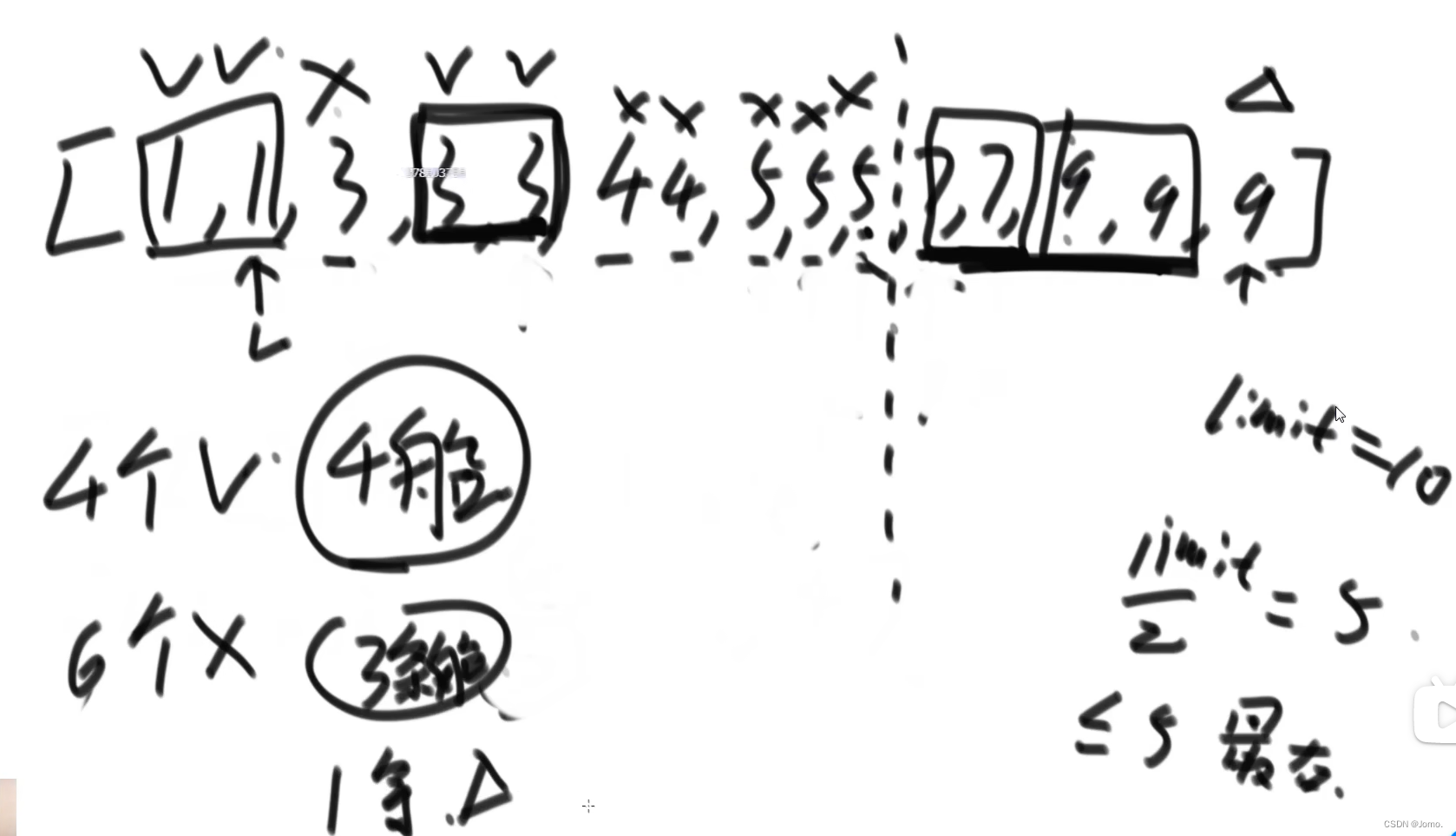
思路：
    1.排序数组，用基数排序（元素（体重）大小范围有限）
    2.找到(limit/2)最右的位置index
      2.1 index==-1，如果元素全都是大于(limit/2)的，至少需要N条船
      2.2 index==arr.size()，如果元素全都是小于(limit/2)的，至少需要N/2条船
    
void radixSort(vector<int>& arr) {
	vector<vector<int>>bucket(10,vector<int>(arr.size()));//二维数组-桶，每个桶就是一个一维数组
	int bucketElementCounts[10] = { 0 };//每个桶里的数据容量
	int max = 0;//待排序数组的最大值
	for (int i = 0; i < arr.size(); i++) {
		if (arr[i] > max) {
			max = arr[i];
		}
	}
	int m_digit = 0;//待排序数组的最大位数
	while (max > 0) {
		m_digit++;
		max /= 10;
	}

	for (int j = 0, n = 1; j < m_digit; j++, n *= 10) {
		for (int k = 0; k < arr.size(); k++) {
			//取出每个元素对应位的值
			int digit = (arr[k] / n) % 10;

			//放入到对应桶中
			bucket[digit][bucketElementCounts[digit]] = arr[k];
			bucketElementCounts[digit]++;
		}

		//按照桶的顺序（一维数组的下标）依次取出数据放回原数组中
		int index = 0;
		for (int l = 0; l < 10; l++) {
			//如果桶中有数据才放入数组
			if (bucketElementCounts[l] != 0) {
				for (int m = 0; m < bucketElementCounts[l]; m++) {
					arr[index] = bucket[l][m];
					index++;
				}
			}
			//为了模拟桶的数据被取出，我们需要将桶中的数据容量清空
			bucketElementCounts[l] = 0;
		}
	}
}

int minBoat(vector<int>arr, int limit) {
	if (arr.size() == 0)return 0;
	radixSort(arr);
	
	if (arr[arr.size() - 1] < (limit / 2))return (arr.size()+1) / 2;//需要向上取整
	if (arr[0] > (limit / 2))return arr.size();
	int lessR = -1;
	for (int i = arr.size()-1; i >= 0; i++) {
		if (arr[i] <= (limit / 2)) {
			lessR = i;
			break;
		}
	}
	
	int L = lessR;
	int R = lessR + 1;
	int lessUnused = 0;
	while (L >= 0) {
		int solved = 0;
		while (R < arr.size() && arr[L] + arr[R] <= limit) {//贪心
			R++;
			solved++;
		}
		if (solved == 0) {
			lessUnused++;
			L--;
		}
		else {
			L = max(-1, L - solved);
		}
	}
	int lessAll = lessR + 1;
	int lessUsed = lessAll - lessUnused;
	int moreSolved = arr.size() - lessR - 1 - lessUsed;
	return lessUsed + ((lessUnused + 1) >> 1) + moreSolved;
}

2.最长回文子序列

int lcse(string str) {
	if (str.length() == 0)return 0;
	vector<vector<int>>dp(str.length(), vector<int>(str.length()));

	for (int i = 0; i < str.length(); i++) {
		dp[i][i] = 1;
	}
	for (int j = 0; j < str.length()-1; j++) {
		dp[j][j + 1] = str[j] == str[j + 1] ? 2 : 1;
	}

	for (int i = str.length() - 2; i >= 0; i--) {
		for (int j = i + 2; j < str.length(); j++) {
			dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
			if (str[i] == str[j]) {
				dp[i][j] = max(dp[i][j], dp[i + 1][j - 1] + 2);
			}
		}
	}
	return dp[0][str.length() - 1];
}

3.最少添加字符让字符串变回文串

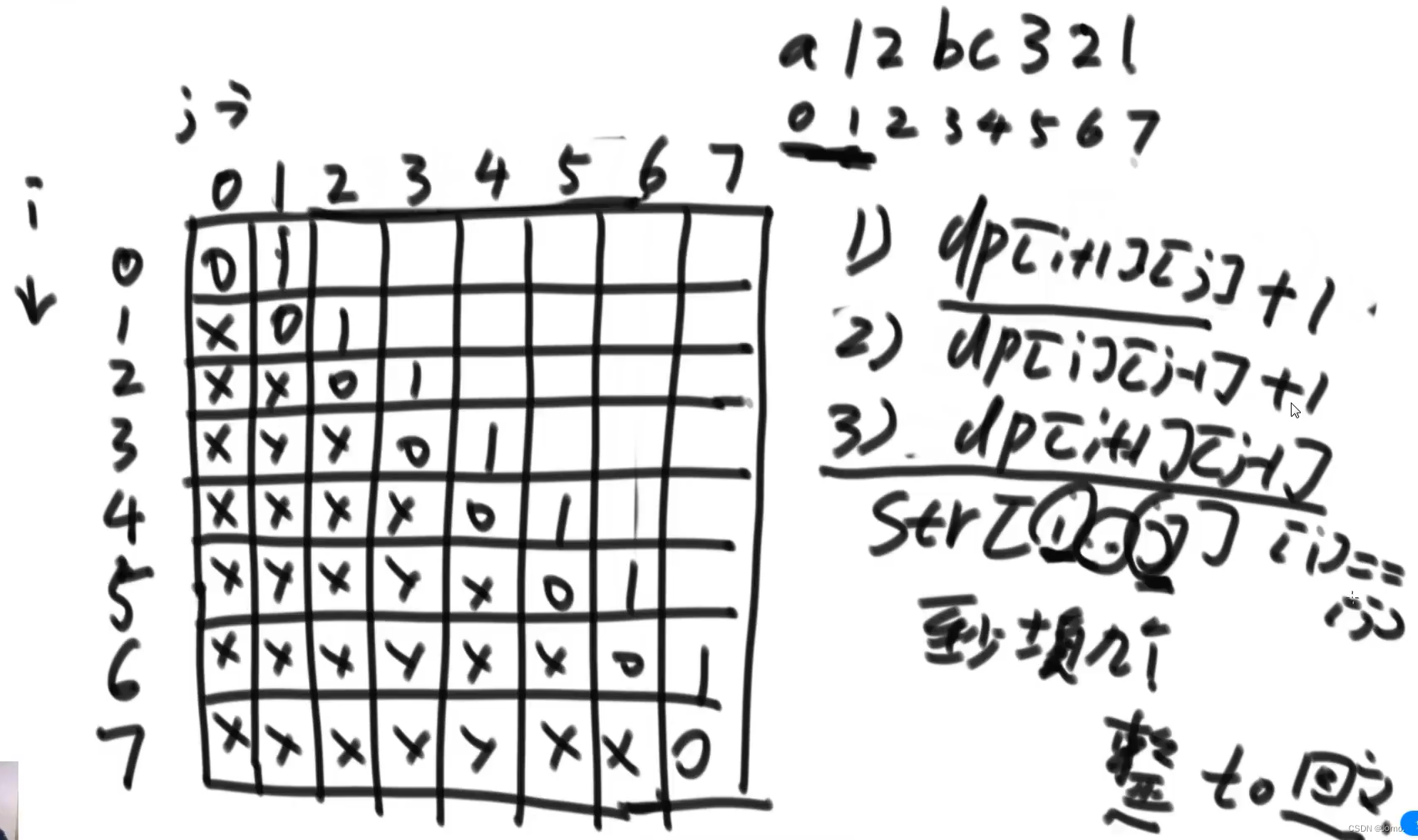
dp[i][j]：至少添几个字符才能让str[i...j]变成回文串
vector<vector<int>>getDp(string str) {
	vector<vector<int>>dp(str.length(), vector<int>(str.length()));
	for (int j = 1; j < str.length(); j++) {
		dp[j - 1][j] = str[j] == str[j - 1] ? 0 : 1;
		for (int i = j - 2; i > -1; i--) {
			if (str[i] == str[j]) {
				dp[i][j] = dp[i + 1][j - 1];
			}
			else {
				dp[i][j] = min(dp[i + 1][j], dp[i][j-1])+1;
			}
		}
	}
	return dp;
}

string getPalindrome(string str) {
	if (str.length() < 2)return str;
	vector<vector<int>>dp = getDp(str);
	string res(str.length() + dp[0][str.length() - 1], '\0');
	int i = 0;
	int j = str.length() - 1;
	int resl = 0;
	int resr = res.length() - 1;
	while (i <= j) {
		if (str[i] == str[j]) {
			res[resl++] = str[i++];
			res[resr--] = str[j--];
		}
		else if (dp[i][j - 1] < dp[i + 1][j]) {
			res[resl++] = str[j];
			res[resr--] = str[j--];
		}
		else {
			res[resl++] = str[i];
			res[resr--] = str[i++];
		}
	}
	return res;
}

4.回文子串的最少切割次数

vector<vector<bool>>record(string str) {
	vector<vector<bool>>record(str.length(), vector<bool>(str.length()));
	record[str.length() - 1][str.length() - 1] = true;
	for (int i = 0; i < str.length() - 1; i++) {
		record[i][i] = true;
		record[i][i + 1] = str[i] == str[i + 1];
	}
	for (int row = str.length() - 3; row >= 0; row--) {
		for (int col = row + 2; col < str.length(); col++) {
			record[row][col] = str[row] == str[col] && record[row + 1][col - 1];
		}
	}
	return record;
}

int minCut(string str) {
	if (str.length() < 2)return str.length();
	int len = str.length();
	vector<int>dp(len + 1);
	dp[len] = 0;//防溢出
	dp[len - 1] = 1;
	vector<vector<bool>>p = record(str);
	for (int i = len - 1; i >= 0; i--) {
		dp[i] = str.length() - i;
		for (int j = i; j < len; j++) {
			if (p[i][j]) {
				dp[i] = min(dp[i], dp[j + 1] + 1);
			}
		}
	}
	return dp[0] - 1;
}

 5.移除字符使字符串变回文串的方案数

dp[i][j]：把以下所有可能性都要算上
(1)以i，以j
(2)不以i，以j
(3)不以i，不以j
(4)以i，不以j
dp[i][j-1]=(3)+(4)
dp[i+1][j]=(2)+(3)
dp[i+1][j-1]=(3)

(2)+(3)+(4)=dp[i][j-1]+dp[i+1][j]-dp[i+1][j-1]
(1)=str[i]==str[j]，dp[i+1][j-1]+1

int ways(string str) {
	int n = str.length();
	vector<vector<int>>dp(str.length(), vector<int>(str.length()));
	for (int i = 0; i < n; i++) {
		dp[i][i] = 1;
		if (i + 1 < n && str[i] == str[i + 1]) {
			dp[i][i + 1] = 3;
		}
		else {
			dp[i][i + 1] = 2;
		}
	}
	for (int p = 2; p < n; ++p) {
		for (int i = 0, j = p; j < n; ++i, ++j) {
			if (str[i] == str[j]) {
				dp[i][j] = dp[i + 1][j] + dp[i][j - 1] + 1;
			}
			else {
				dp[i][j] = dp[i + 1][j] + dp[i][j - 1] + dp[i + 1][j - 1];
			}
		}
	}
	return dp[0][n - 1];
}