二、背景资料

        在这篇文章中，我们将研究带有梯度惩罚的Wasserstein GAN。虽然最初的Wasserstein GAN[2]提高了训练稳定性，但仍存在生成较差样本或无法收敛的情况。回顾一下，WGAN的成本函数为：

公式 1：WGAN 值函数。

        其中 f 是 1-利普希茨连续的。WGAN的问题主要是因为用于对批评者强制执行Lipschitz连续性的权重裁剪方法。WGAN-GP用对批评家的梯度范数的约束代替了权重裁剪，以强制执行Lipschitz的连续性。这允许比WGAN更稳定的网络训练，并且需要很少的超参数调优。WGAN-GP和这篇文章建立在Wasserstein GANs之上，这已经在揭秘系列的上一篇文章中讨论过。查看下面的帖子以了解 WGAN。

报表 1

可微的最优1-Lipschitz函数，最小化方程1的f*在Pr和Pg下几乎在任何地方都有单位梯度范数。

Pr 和 Pg 分别是真假分布。语句 1 的证明可以在 [1] 中找到。

三、渐变剪切问题

3.1 容量未充分利用

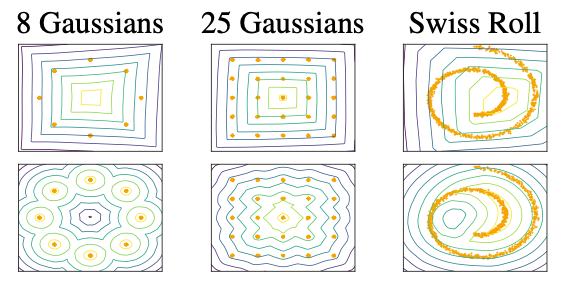
图2：WGAN评论家（上）使用梯度裁剪学习的值表面，（下）使用梯度惩罚学习的值表面。图片来源： [1]

使用权重裁剪来强制执行 k-Lipschitz 约束会导致批评者学习非常简单的函数。

从语句 1 中，我们知道最优批评者的梯度范数在 Pr 和 Pg 中几乎无处不在都是 1。在权重裁剪设置中，批评家试图达到其最大梯度范数 k，并最终学习简单的函数。

图2显示了这种效果。批评者被训练收敛固定生成分布（Pg）作为实际分布（Pr）+单位高斯噪声。我们可以清楚地看到，使用权重裁剪训练的批评家最终学习了简单的函数并且未能捕捉到更高的时刻，而使用梯度惩罚训练的批评家则没有这个问题。

3.2 梯度爆炸和消失

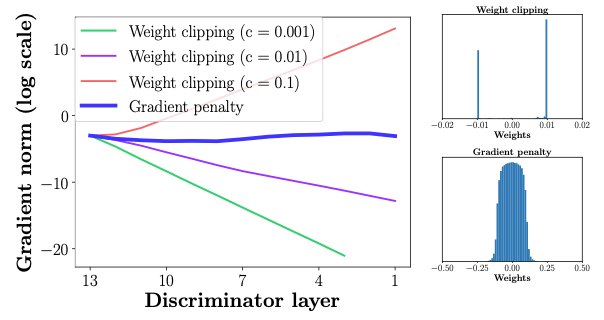
权重约束和损失函数之间的相互作用使得WGAN的训练变得困难，并导致梯度爆炸或消失。

这在图1（左）中可以清楚地看到，其中注释器的权重在不同的削波值下爆炸或消失。图 1（右）还显示，渐变削波将注释器的权重推到两个极端削波值。另一方面，接受梯度惩罚训练的批评家不会遇到此类问题。

四、梯度惩罚

梯度惩罚的想法是强制执行一个约束，使得批评者输出的梯度与输入具有单位范数（语句 1）。

作者提出了该约束的软版本，对样本x̂∈Px̂的梯度范数进行惩罚。新目标是

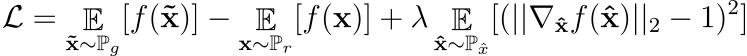
公式2：批评家损失函数

在方程 2 中，总和左侧的项是原始批评者损失，总和右侧的项是梯度惩罚。

Px̂ 是通过在实分布和生成的分布 Pr 和 Pg 之间沿直线均匀采样而获得的分布。这样做是因为最优注释器在从Pr和Pg耦合的样品之间具有单位梯度范数的直线。

λ，惩罚系数用于对梯度惩罚项进行加权。在论文中，作者为所有实验设置了λ = 10。

批规范化不再在注释中使用，因为批范数将一批输入映射到一批输出。在我们的例子中，我们希望能够找到每个输出的梯度，w.r.t它们各自的输入。

五、代码示例

5.1 梯度惩罚

 梯度惩罚的实现如下所示。

def compute_gp(netD, real_data, fake_data):
        batch_size = real_data.size(0)
        # Sample Epsilon from uniform distribution
        eps = torch.rand(batch_size, 1, 1, 1).to(real_data.device)
        eps = eps.expand_as(real_data)
        
        # Interpolation between real data and fake data.
        interpolation = eps * real_data + (1 - eps) * fake_data
        
        # get logits for interpolated images
        interp_logits = netD(interpolation)
        grad_outputs = torch.ones_like(interp_logits)
        
        # Compute Gradients
        gradients = autograd.grad(
            outputs=interp_logits,
            inputs=interpolation,
            grad_outputs=grad_outputs,
            create_graph=True,
            retain_graph=True,
        )[0]
        
        # Compute and return Gradient Norm
        gradients = gradients.view(batch_size, -1)
        grad_norm = gradients.norm(2, 1)
        return torch.mean((grad_norm - 1) ** 2)

5.2 关于WGAN-GP代码

训练 WGAN-GP 模型的代码可以在这里找到：

5.3 输出

        图例.3显示了训练WGAN-GP的一些早期结果。请注意，图 3 中的图像是早期结果，一旦确认模型按预期训练，训练就会停止。该模型未经过训练以收敛。

六、结论

        Wasserstein GAN 在训练生成对抗网络方面提供了急需的稳定性。但是，使用梯度削波导致各种问题，例如梯度爆炸和消失等。梯度惩罚约束不受这些问题的影响，因此与原始WGAN相比，允许更容易的优化和收敛。这篇文章研究了这些问题，介绍了梯度惩罚约束，还展示了如何使用 PyTorch 实现梯度惩罚。最后，提供了训练WGAN-GP模型的代码以及一些早期阶段的输出。阿迪西亚·桑卡尔