一、根据二叉树创建字符串

题目链接：力扣第606题：根据二叉树创建字符串

解析：

这道题主要是关于二叉树的前序遍历，题目要求我们的每一个子树都要用括号括起来，然后要求最终要删除重复的括号，那么我们先来解决最基本的，将括号都括起来再说，然后再讨论如何去除多余括号

我们很容易想到如下的方法可以先将每个都带上括号。就是一个先序遍历，需要注意的就是to_string这个函数也许不是那么的常见，它的作用是将一个整型转换为string类型的。

我们先观察一下测试结果，跟我们预期是一样的。现在主要关心的是除去多余的括号

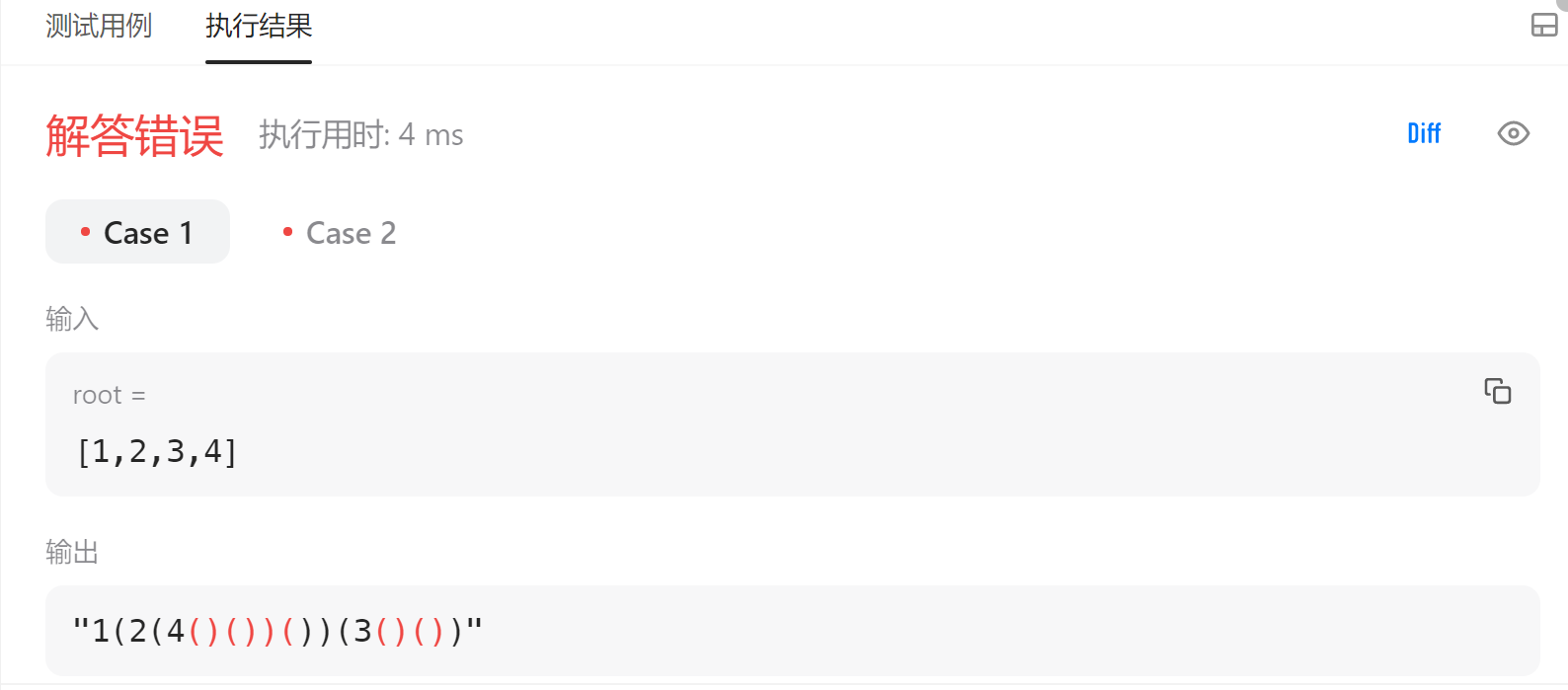
对于除去多余的括号，我们可以先讨论一下，何时加上括号？根据原题的样例，我们不难得知

如果左子树不为空且右子树为空，可以省略右子树的括号，只要输出左子树的括号
如果左子树为空且右子树不为空，不可以省略左子树的括号，左右都要输出
如果两个子树都为空，两个括号都要省略，都不输出左右子树的括号
如果两个都不为空，两个都不省略，左右都要输出

上面的四条规则，根据我们现有的代码，我们可以考虑何时不省略括号的条件即可，只要当不省略的条件满足，就正常加入括号即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string tree2str(TreeNode* root) {

        if(root==nullptr)
        {
            return "";
        }
        string str;
        str+=to_string(root->val);

        if((root->left&&root->right==nullptr)||
           (root->left&&root->right)||
           (root->left==nullptr&&root->right))
        {
            str+='(';
            str+=tree2str(root->left);
            str+=')';

        }
        if((root->left==nullptr&&root->right)||(root->left&&root->right))
        {
            str+='(';
            str+=tree2str(root->right);
            str+=')';
        }
        return str;
    }
};

上面的代码是可以通过的，不过上面的条件显得过于臃肿了，我们不妨简化一下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string tree2str(TreeNode* root) {

        if(root==nullptr)
        {
            return "";
        }
        string str;
        str+=to_string(root->val);

        if((root->left||root->right))
        {
            str+='(';
            str+=tree2str(root->left);
            str+=')';

        }
        if(root->right)
        {
            str+='(';
            str+=tree2str(root->right);
            str+=')';
        }
        return str;
    }
};

二、二叉树的最近公共祖先

力扣链接：力扣第236题：二叉树的最近公共祖先

解析：

对于这道题，如果这道题是一个三叉链的话，就很简单了，因为就相当于退化为了两个链表的相交问题，此时我们直接计算长度，然后使用快慢指针即可。这样就很简单了。不过可惜的是这道题是二叉链的。所以上面的想法是不可以的。

1.解法一：递归

这道题，我们先来画图熟悉一下公共祖先的几种可能性

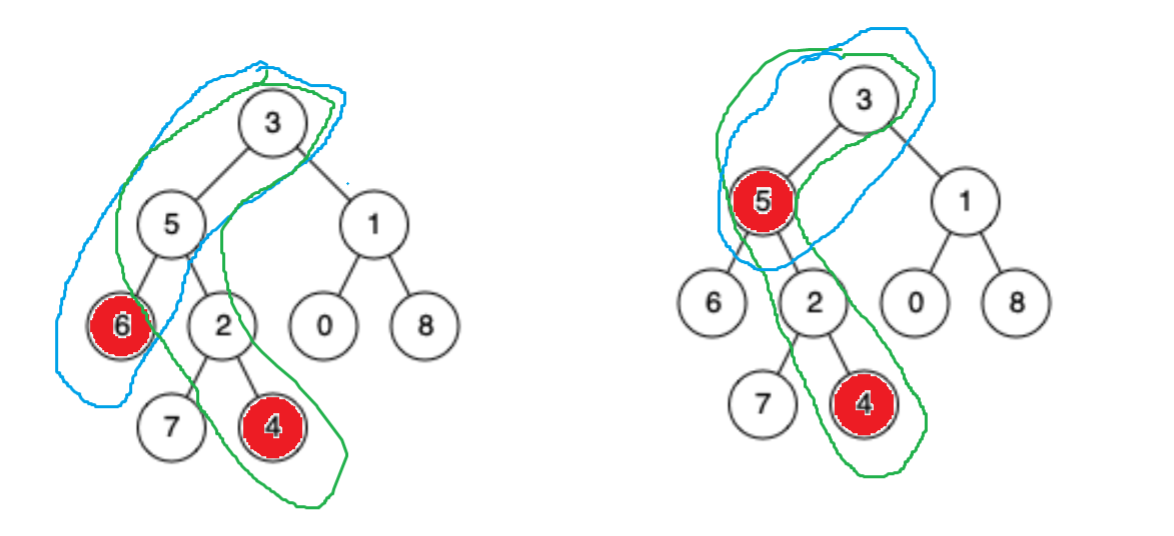
如上图所示，所有的可能性就两种，一种是如果是4和6的情况下，他们所处的路径上，最近的就是5，此时我们会注意到，对于5这个结点而言，一个在左边，一个在右边。如果是更远一点的公共祖先的话，就不满足这种情况了。要么都在祖先的左边，要么都在祖先的右边。通过这一点，我们就知道了一种祖先的判别方式。还有一种情况就是一个结点是另外一个结点的祖先，如由上图所示。这时候满足的条件就是，如果此时root就等于p或者q的话，那么root就是我们的公共祖先了。

依据上面的分析，我们可以写出如下代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool FindNode(TreeNode* root, TreeNode* obj)
    {
        if(root==nullptr)
        {
            return false;
        }
        if(root == obj)
        {
            return true;
        }
        return FindNode(root->left,obj)||FindNode(root->right,obj);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr)
        {
            return nullptr;
        }
        if(root == p || root == q)
        {
            return root;
        }
        bool pInLeft,pInRight,qInLeft,qInRight;
        pInLeft = FindNode(root->left, p);
        pInRight = !pInLeft;
        qInLeft = FindNode(root->left ,q);
        qInRight = !qInLeft;
        if(pInLeft&&qInLeft)
        {
            return lowestCommonAncestor(root->left,p,q);
        }
        else if(pInRight&&qInRight)
        {
            return lowestCommonAncestor(root->right,p,q);
        }
        else 
        {
            return root;
        }

    }
};

时间复杂度分析：

这道题的时间复杂度是O(N²)，因为最极端的情况如下所示，即二叉树已经退化为了一个链表，这时候，二叉树高度为N，且由于每次都在一边，这需要N次。在每一次中，又需要判断是不是在左树，这个判断是一个等差数列。所以最终的时间复杂度为O(N²)。不过主要的原因还是在于这是一颗普通的树，假如这棵树是一棵二叉搜索树，那么我们的代价就变小了很多。我们Find的代价直接就没有了，因为根据性质我们就可以知道某个结点是在左子树还是右子树。所以效率变为了O(N)

2.解法二：借助栈来寻找路径

我们一开始想的办法是如果是三叉链的话，那么就可以转化为链表相交的问题，那么如果不是三叉链的话有没有办法能实现类似的思路呢？答案是有的，我们三叉链相比二叉链的优势就是三叉链可以很方便的找到路径。然后根据路径遇到相同的就是最近公共祖先了。

而对于二叉链，我们就只能使用栈来寻找路径了。只要有了路径，那么就可以采用类似的思路了。

所以我们就可以写出如下代码了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool FindPath(TreeNode* root, TreeNode* obj, stack<TreeNode*>& st)
    {
        if(root == nullptr)
        {
            return false;
        }
        st.push(root);        
        if(obj == root)
        {
            return true;
        }
        if(FindPath(root->left,obj,st))
        {
            return true;
        }
        if(FindPath(root->right,obj,st))
        {
            return true;
        }
        st.pop();
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> pst;
        FindPath(root,p,pst);
        stack<TreeNode*> qst;
        FindPath(root,q,qst);

        while(pst.size()>qst.size())
        {
            pst.pop();
        }
        while(pst.size()<qst.size())
        {
            qst.pop();
        }
        while(pst.top()!=qst.top())
        {
            pst.pop();
            qst.pop();
        }
        return pst.top();
    }
};

在这段代码中，尤其是寻找路径这段代码，是非常巧妙的，它是利用了返回值的真假来进行截断的。否则我们很难控制路径的结束。

三、二叉搜索树与双向链表

牛客链接：牛客：二叉搜索树转化为双向链表

解析：

这道题我们最容易想到的办法就是暴力法，即直接用一个栈，将每一个结点都放到栈里面。然后再依次将每个结点链接起来即可。不过很可惜，这道题具有空间复杂度要求。显然不想让我们使用任何容器，想让我们就在原地进行修改链接关系。

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
	void InOrder(TreeNode* root, TreeNode*& prev)
	{
		if(root == nullptr)
		{
			return;
		}
		InOrder(root->left,prev);
		root->left = prev;
		if(prev)
		{
			prev->right = root; 
		}
		prev = root;
		InOrder(root->right,prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {
		if(pRootOfTree==nullptr)
		{
			return nullptr;
		}
		TreeNode* ret = pRootOfTree;
		while(ret->left)
		{
			ret = ret->left;
		}
		TreeNode* prev = nullptr;

        InOrder(pRootOfTree,prev);

		return ret;
    }
};

如上代码所示，既然要是排序的双向链表，那么必然是中序的。在中序的过程中，我们需要改变链接关系，只传一个指针是肯定不够的，虽然我们是无法窥测未来的，但是过去我们是知道的，所以我们应该传一个前驱节点，然后让当前的左指向过去，过去的右指向现在。然后将过去的值赋为现在，就可以继续下一次递归了。

四、前序与中序构建二叉树

力扣链接：力扣第105题:前序与中序构建二叉树

解析：

这道题的思路我们还是比较清楚的，根据前序确定根，然后再中序中确定根所处的位置，分割两个区间，然后递归即可。

但是再一些细节把握上还是需要注意的，递归戒截止的条件应该是当左右不构成区间了那么递归就该结束了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* build(vector<int>& preorder,vector<int>& inorder,int& previ,int inbegin,int inend)
    {
        if(inbegin>inend)
        {
            return nullptr;
        }
        TreeNode* newnode = new TreeNode(preorder[previ]);
        int inpos = inbegin;
        while(inpos<=inend)
        {
            if(preorder[previ]==inorder[inpos])
            {
                break;
            }
            inpos++;
        }
        previ++;
        newnode->left = build(preorder,inorder,previ,inbegin,inpos-1);
        newnode->right = build(preorder,inorder,previ,inpos+1,inend);
        return newnode;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int previ = 0;
        return build(preorder,inorder,previ,0,inorder.size()-1);
    }
};

五、中序与后序构建二叉树

力扣链接：力扣第106题：中序与后序构建二叉树

解析：

这道题与前面的题基本上是一样的。后序与前序的不同就是我们创建好结点以后，就得先创建右子树了，才能创建左子树。这是因为后序是左子树，右子树，根这种遍历方式的，那么越靠后就先是右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    TreeNode* build(vector<int>& inorder,vector<int>& postorder,int& posti,int inbegin,int inend)
    {
        if(inbegin>inend)
        {
            return nullptr;
        }
        TreeNode* newnode = new TreeNode(postorder[posti]);
        int inpos = inbegin;
        while(inpos<inend)
        {
            if(postorder[posti]==inorder[inpos])
            {
                break;
            }
            inpos++;
        }
        posti--;
        newnode->right = build(inorder,postorder,posti,inpos+1,inend);
        newnode->left = build(inorder,postorder,posti,inbegin,inpos-1);
        return newnode;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int posti = postorder.size()-1;
        return build(inorder,postorder,posti,0,inorder.size()-1);
    }
};