2022年全国研究生数学建模竞赛华为杯
A题 移动场景超分辨定位问题
原题再现:
在日常家庭生活中,人们可能需要花费大量时间去寻找随意摆放在家中某些角落里的小物品。但如果给某些重要物品贴上电路标签,再利用诸如扫地机器人的全屋覆盖能力,可以精准定位到这些物体,将极大地提升人们生活的便利性。而在智能辅助驾驶或者自动驾驶领域,更需要精准探测邻近车辆、行人的位置及速度,来控制车速、转向和刹车等以免发生意外。这些都属于移动场景定位问题。显然,定位的精度越高,应用价值越大,特别是超分辨率定位,具有广阔的应用前景。
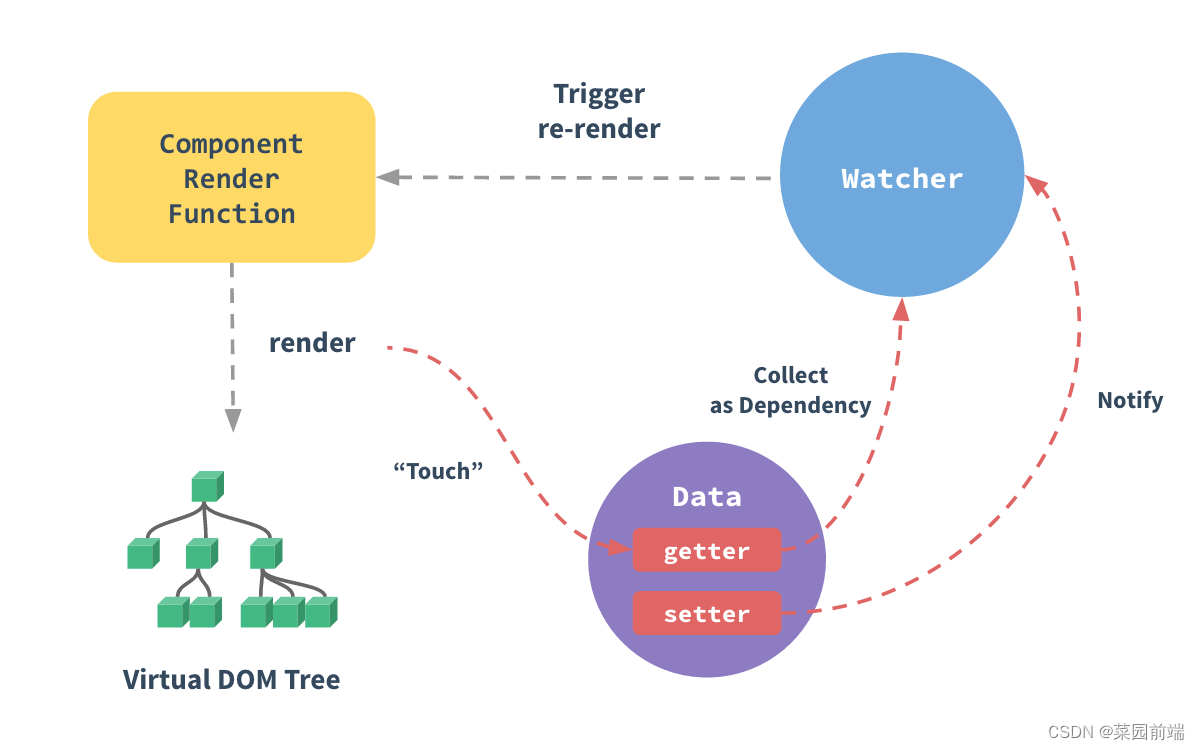
现有移动场景定位产品通常采用调频连续波雷达FMCW (frequency-modulated continuous-wave) ,通过发射线性增长频率的信号波,以及接收反射回来的信号波来进行定位,示意图如下
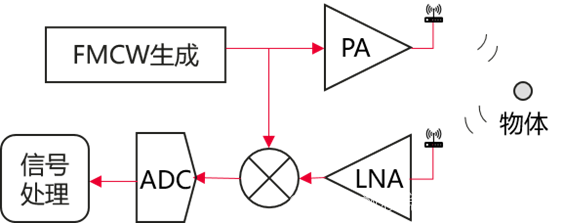
其中PA(Power Amplifier),LNA(Low Noise Amplifier),ADC(Analogue-to-Digital Converter)。现有产品大多采用基线算法,其得到的分辨率较低,不能满足日益增长的超分辨定位需求,亟需通过建模以及设计对应算法来提高分辨率,以提升产品竞争力。
为了简化,我们考虑平面二维场景。假设在一个chirp周期T内,雷达发射信号的频率及发射波信号分别为
f(t)=f_0+γt,0≤t<T
s_TX (t)=A_TX exp(j2π( f_0 t+γ/2 t^2 )),0≤t<T
其中A_TX表示信号发射功率,f_0表示载频,γ表示调频斜率,T表示chirp周期,j表示虚数单位。则雷达经过距离为R_0的物体反射后的接收信号为
s_RX (t)=A_RX exp(j2π( f_0 (t-τ)+γ/2 (t-τ)^2 )),τ≤t<T
其中A_RX表示信号接收功率,τ=2R_0/c为接收时延,这里c表示光速。发射信号和接受信号在[τ,T]上有重叠,将这两个信号输入混频器,即可得到中频(IF)信号
s_IF (t)=s_TX (t) s_RX^* (t)=A_TX A_RX exp(j2π(γτt+ f_0 τ)),τ<t≤ T.
其中忽略了τ^2(τ≪1) 项。由于中频信号的频率为f_IF=γτ,故R_0=c/2γ f_IF.
在水平面上,孔径为L的N_a个等效虚拟天线阵列是均匀排布的。我们建立以天线阵列中心为原点的坐标系,天线阵列为x轴,垂直于天线阵列的是y轴。
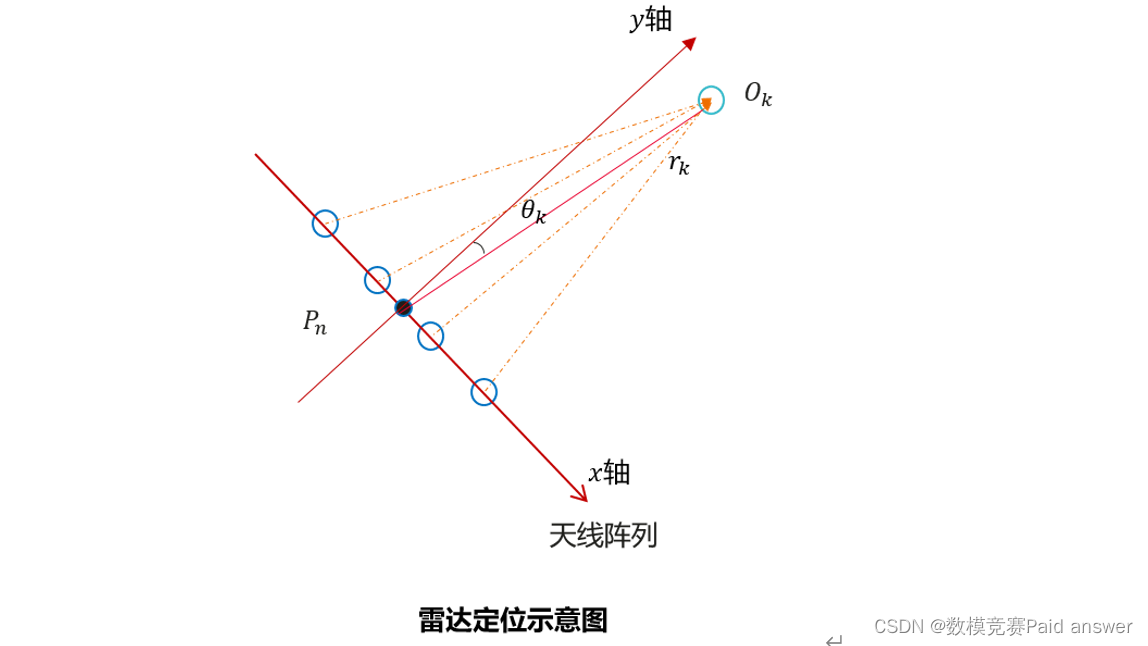
假设物体O_k到中心距离为r_k,且与y轴的夹角θ_k,则对应的坐标为
X_k=r_k sinθ_k,Y_k=r_k cosθ_k
因此第n根天线(坐标为:{x_n=-L/2+nL/(N_a-1),y_n=0}, n=0,1,⋯,N_a-1.) 的双程回波距离为
R_(n,k)=2√((x_n-X_k )^2+(y_n-Y_k )^2 )
对于这样回波距离的物体,FMCW雷达在时刻t,第n根天线上的接收中频信号为(这里及之后要关于时刻做均匀采样,为简化公式用T_s t来表示t)
s_(n,k) (t)=a_k e^j(2πγT_s tτ+2πf_0 τ)
=a_k e^j(2πγ T_s t R_(n,k)/c +2π f_0 R_(n,k)/c) ,t=0,1,2,⋯,[T/T_s ]-1
其中a_k表示物体的反射性,T_s是采样间隔,c为光速,[T/T_s ]表示取整。 在一个chirp周期内的时刻t,第n根天线接受到的中频信号是由K个目标物体带噪声中频信号的混合
z_n (t)=∑_(k=1)^K▒〖s_(n,k) (t)+w_n (t)〗,t=0,1,2,⋯,[T/T_s ]-1
这里w_n表示噪声。
在移动场景中,雷达获得一帧(N_f个chirp周期)中频信号组{Z_q,q=0,⋯,N_f-1}。 这里对于任意给定的q,中频信号Z_q={z_n (t),n=0,⋯,N_a-1,t=0,⋯,[T/T_s ]-1}表示第q个chirp周期内采集的信号,由于chirp周期(~50微秒)内时间极短,可认为此周期内物体静止不变。在一帧时间内,物体的相对位置有明显的移动。
移动场景超分辨率定位是指:在上述移动场景下,设计鲁棒的低复杂度在线算法,实时超分辨率定位到物体。(不妨假设天线半径远小于物体的距离)
现有算法及研究现状:
现有产品中基线算法是通过加Hamming窗,然后做FFT来测距、测角。优点是复杂度低,缺点是分辨率较低。
传统算法如MUSIC算法,通过空间平滑化滤波以及特征子空间的分解来分离信号空间和噪声空间,但是也会造成分辨率下降以及受噪声的较大干扰。
现有的压缩感知算法利用了空间物体分布的稀疏性,可以有效提升分辨率,但处理这种连续傅里叶字典场景并设计低复杂度算法是一个巨大的挑战。
问题:
1.针对提供的无噪声仿真数据,建立定位模型,计算出物体相对位置,并以二维极坐标图(横坐标表示距离,纵坐标表示角度)展示。
2.针对提供的高斯噪声仿真数据,利用一个chirp周期内的IF信号,设计超分辨算法精确定位多个物体。
3.设计在线低复杂度算法,利用一帧中频信号来超分辨定位,并且通过数值实验验证算法性能。针对提供的一帧数据,计算出物体相对运动轨迹,并以二维图(横坐标表示距离,纵坐标表示角度)展示。
4.考虑实际场景中由于老化等原因,天线阵列对于自身的定位也会有误差。针对提供的仿真数据,设计提升定位算法的鲁棒性的改进算法。
整体求解过程概述(摘要)
在日常家庭生活中,人们可能需要花费大量的时间去寻找随意摆放在家中某些角落的小物品。但如果给某些重要物品贴上电路标签,再利用诸如扫地机器人的全屋覆盖能力,可以精确定位到这些物体,这将极大地提升人们生活的便利性。在自动驾驶或者智能辅助驾驶领域,毫米波雷达作为一个重要的辅助工具已经应用到汽车驾驶中。这些场景更需要精确探测邻近车辆、行人的位置及速度,以便控制车速、转向和刹车防止发生意外。这些都属于移动场景定位问题。如何提升毫米波雷达的角分辨率就成为一个亟需解决的问题。显然,定位的精度越高,应用价值越大,特别是高分辨定位,拥有广阔的应用前景。
针对问题一,本节分析出题目采用两发四十三收的 FCMV-MIMO 雷达体制并给出其中一种可能的系统结构。基于该体制建立 FCMV 信号模型、FCMV-MIMO 等效虚拟孔径雷达模型,对目前工程上常用的基线法测距测角进行原理分析。针对基线法测角分辨力不高的缺陷,引入基于盖尔圆的 MUSIC算法进行超分辨 DOA 估计。综合以上两个算法,本节采用基线法测距、盖尔圆 MUSIC 算法测角实现联合定位,并给出定位结果:目标 1距离阵列相位中心 7.0303m,与阵列垂直方向夹角为 0.0011°;目标2 距离阵列相位中心 7.0303m,与阵列垂直方向夹角为 0.1334°。
针对问题二,考虑到 MUSIC 算法在低信噪比情况下性能急剧恶化,本节建立基于压缩感知的DOA 估计模型,并提出基于修正 L1-SVD 混合范数约束的 CS-DOA 估计算法。通过迭代正则化参数有效消除经典 CS 算法中多目标临近带来的伪峰效应,提高超分辨测角能力。最终给出多目标定位结果:目标 1 距离阵列相位中心 8.2218m,与阵列垂直方向夹角为-0.71°;目标 2 距离阵列相位中心 8.2218m,与阵列垂直方向夹角为 0.71°。
针对问题三,鉴于压缩感知类算法处理连续傅里叶字典场景复杂度过高,本节采用基于子空间旋转变换的快速 DOA 估计算法,能够实现在线目标定位。同时针对超分辨算法定位求解带来的距离、角度二值映射问题,提出三维联合、基线法预处理两种目标匹配定位算法。最终给出 32 个 chirp 周期的定位结果并绘制目标运动轨迹。
针对问题四,本节首先采用基于特征空间的幅相误差和角度联合迭代优化方法校正阵元幅相误差,得到目标精确定位结果:目标 1 距离阵列相位中心 6.1246m,与阵列垂直方向夹为-0.1040°;目标 2 距离阵列相位中心 6.0056m,与阵列垂直方向夹角为 0.1210°。同时,基于通道间相差平衡思想,本文创新性地构建了空间相位恒定因子,并提出联合相位误差自适应预校正和 MUSIC 的 DOA 估计算法,较好地实现对幅相误差的校正,得到了相应的目标高精度定位结果:目标 1 距离阵列相位中心 6.1246m,与阵列垂直方向夹角为-0.1053°;目标 2 距离阵列相位中心6.0056m,与阵列垂直方向夹角为 0.1183°。
模型假设:
通过分析题目,本文已有设定如下:
1. 实际 MIMO 雷达通过联合发射与接收构建虚拟天线阵列,由于接收后中频数据已经给出,因此本文将不考虑具体发射情况,而主要从信号处理的角度进行超分辨定位问题求解。
2. 天线半径远小于物体的距离,即认为目标处于阵列孔径远场范围。
3. 在各个场景下,均假设有 K 个需要分析确定的物体在雷达的探测范围内,该探测范围是以原点为中心半径 10 米以内、开口向上张开角为100° 的扇形区域。
4. 由于实际雷达对目标在空间是三维探测,包括俯仰、方位、距离三个维度。本文仅考虑目标相对于阵列的距离、角度二维定位情况。
5. 在移动场景下,目标相对雷达发生运动。雷达获得一帧(32 个 chirp 周期)中频信号组,由于chirp 周期内时间极短,可认为在该时间内目标静止不动。而一帧时间里,由于目标运动状态发生改变,因此目标的位置发生偏移。
6. 本题目中涉及到噪声均为高斯白噪声,不包括色噪声或其他类型噪声。
问题分析:
问题一分析:
近年来,得益于半导体技术的进步和物联网的普及,搭载毫米波技术的设备开始进入普罗大众的生活,如实现手势识别、人体健康信息监测的毫米波雷达。这些设备仅利用了毫米波雷达的距离信息和多普勒信息,通过引入 MIMO 技术后,MIMO 雷达通过等效虚拟阵列在空间上扩充了阵元。由于这些特性,在理论上毫米波雷达更容易设计成大规模的阵列,进而获得很高的方位向分辨率能力。针对问题一需要建立的定位模型及其求解,这里明确定位包括距离测量和角度估计层级,同时角度估计在阵列信号处理领域也称波达方法估计,即常见的 DOA 估计。因此距离测量和 DOA 估计一起归于定位技术范畴。问题一的核心是通过处理题目给出的无噪声数据,计算出物体相对于阵列的位置,实现目标定位。因此,本节首先需要对给出的 data_q1.mat 进行数据分析,并利用题目已知的参数推算出出FCMV-MIMO 雷达系统结构。后文将基于该结构进行 FCMV 信号模型、FCMV -MIMO 雷达等效虚拟孔径模型等基础模型的建模。通过对基础模型的建立将有助于加强对 data_q1.mat 数据的理解。本节将设计联合基线-MUSIC 方法,实现对目标的精确定位并最终通过表格和极坐标图的形式展示对目标的定位结果。
问题二分析:
传统的空间谱估计方法存在各种不足,同时考虑到空域信号本身特有的稀疏特性。采用压缩感知采样理论的稀疏采样,用低于奈奎斯特定理的采样率获取数据,同时使用合适的稀疏重构算法重构出稀疏信号,所以可以弥补传统阵列测向估计的缺陷,在一定程度上也能增加算法的分辨率以及鲁棒性,而且对于任何类型的信源都适用,不必考虑信源相干/非相干对阵列测向算法的影响,以下对阵列测向也称 DOA 估计。
问题三分析:
从问题 1 和问题 2 算法分析可知,高分辨测角算法联合基线法测距方法如果测得目标位于不同距离单元,需要解决目标匹配问题。如果目标处于同一距离单元,基线法测距、高分辨测角可以得到较为精确的定位结果。由于问题三是一帧共 32 个 chirp 周期时间,目标发生运动,需要考虑合适的目标匹配方法。思路一是联合阵列维、快拍维和 chirp 周期维共 3 个维度,利用到目标运动趋势,因而可以区分出多目标;思路二是认为单个 chirp 周期物体静止不变,相当于 32 个 chirp 周期单独定位。这种情况下,就需要先利用二维 FFT 预处理目标信息,得到目标的粗估计,再分别利用距离 FFT、高分辨测角以及与预处理结果的目标匹配,经过以上步骤最终得到目标的定位结果。由于本题要求兼顾低复杂度和超分辨测角,如果采用预处理再匹配无疑会增加时间消耗,因此本节采用思路一,联合三维信息区分多目标,通过仿真得到 32 个定位结果,并在极坐标系中绘制出目标的运动轨迹。
问题四分析:
实际场景下,由于天线受到干扰等因素的影响或者天线自身由于标准不准引起的幅相误差,天线阵列的角度估计会存在一定偏差。因为这些误差的存在,对 MIMO 雷达系统角度估计精度产生很大的影响。为了提升误差存在情况下的阵列定位问题,这要求在建模的过程中需要尽可能得使系统误差得到补偿。
模型的建立与求解整体论文缩略图



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
clear all;
close all;
clc;
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 2022 年 10 月 6 日
%% question one
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 系统参数
c = 3e8; %光速
Ts = 1.25e-7; %采样周期
fs = 1/Ts; %采样频率(8M)
T = 3.2e-5; %chirp 周期
Nf = 32; %一帧有 32 个 chirp
L = 0.0815; %每个虚拟孔径的长度
gama = 78.986e12; %调频率
Na = 86; %阵元个数
f0 = 78.8e9; %中心频率
POINT_NUM = 256; %点数
lmda = c/f0; %波长
B = gama*T; %chirp 带宽
dd = 2*L/(Na-1); %阵元间距
%% 导入数据
load('data_q1.mat');
%% 1.基线法求解
R0_x = (0:fs/(POINT_NUM-1):fs)*c/(2*gama); %距离维度坐标
theta_y=-90:180/(128-1):90; %角度维度坐标
mm =abs(fftshift((fft((fft(Z,[],2)),128,1)),1)); %基线法
figure(1)
mesh(R0_x,theta_y,mm); %画出 R-thita 图
axis([0 10 -90 90]) %坐标限制
% xlabel('距离/m'); ylabel('角度/°'); zlabel('幅度');
% axes('Position',[0.4 0.3 0.3 0.25])
% mesh(R0_x(118:120),theta_y(60:70),mm(60:70,118:120))
% xlabel('距离/m'); ylabel('角度/°'); zlabel('幅度');
% colormap Jet
win = hann(length(mm(1,:)));
win = repmat(win,1,128).';
mm_hanming = mm.*win;
figure(2)
mesh(R0_x,theta_y,mm_hanming); %画出 R-thita 图
axis([0 10 -90 90]) %坐标限制
xlabel('距离/m'); ylabel('角度/°'); zlabel('幅度');
xlabel('距离/m'); ylabel('角度/°'); zlabel('幅度');
axes('Position',[0.4 0.3 0.3 0.25])
mesh(R0_x(118:120),theta_y(60:70),mm(60:70,118:120))
xlabel('距离/m'); ylabel('角度/°'); zlabel('幅度');
colormap Jet
plot(theta_y,mm(:,119));hold on;grid on;
xlabel('角度/°'); ylabel('幅度');
%% 2.MUSIC 算法求解目标方位角
thita = 0:0.0001:180; %角度搜索范围
d = 0:dd:(Na-1)*dd;
R=Z*Z'/POINT_NUM; %信号的自相关函数
[EV,D]=eig(R); %相关函数特征值分解
EVAq=diag(D)'; %对角矩阵重拍
[EVA,I]=sort(EVAq); %特征值排序
EVA=fliplr(EVA); %特征值反褶
EV=fliplr(EV(:,I)); %特征向量反褶
P = EV(:,4:end); %提取噪声子空间
for i=1:length(thita) %谱峰搜索
A=exp(j*2*pi*d/lmda*cos(thita(i)*pi/180)).';
S(i)=1/(A'*P*P'*A);
end
thita = thita - 90;
out = Peak_Seek(thita,S,2);
figure(2)
plot(thita,20*log10(abs(S)/max(abs(S))),'r');hold on; %将谱峰功率转换成 dB
grid on;hold on;
axis([-50 50 -90 0]) %坐标限制
title('MUSIC 测角')
xlabel('目标方位(度)')
ylabel('输出功率(dB)')
axes('Position',[0.4 0.3 0.3 0.25])
% plot(theta_y(60:70),mm(60:70,119));
plot(thita(1800000/2-2000:1800000/2+3340),20*log10(abs(S(1800000/2-
2000:1800000/2+3340)/max(abs(S)))),'r');hold on; %将谱峰功率转换成 dB
xlabel('目标方位(度)')
ylabel('输出功率(dB)')
colormap Jet
axis([-0.2 0.4 -33 0])
clear all;
close all;
clc;
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 2022 年 10 月 7 日
%% question two
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 系统参数
c = 3e8; %光速
Ts = 1.25e-7; %采样周期
fs = 1/Ts; %采样频率(8M)
T = 3.2e-5; %chirp 周期
Nf = 32; %一帧有 32 个 chirp
L = 0.0815; %每个虚拟孔径的长度
gama = 78.986e12; %调频率
Na = 86; %阵元个数
f0 = 78.8e9; %中心频率
POINT_NUM = 256; %点数
lmda = c/f0; %波长
B = gama*T; %chirp 带宽
dd = 2*L/(Na-1); %阵元间距
%% 导入数据
load('data_q2.mat');
%% 1.L1-SVD 求解
K = 2; %信源数
%snapshot= size(Z_noisy,2); %快拍数
snapshot=256;
X=Z_noisy;
Searching_doa=-50:0.01:50;
for m=1:length(Searching_doa)
AA(:,m) = exp(-1j*(0:Na-1)*dd*2*pi*sin(Searching_doa(m)*pi/180)/lmda); %构造一度为网格间距的
完备基矩阵
end
Y=X; %得到观测数据矩阵
Dk1=eye(K);
Dk2 = zeros(K,snapshot-K);
Dk = [Dk1,Dk2].';
[U,D,V] = svd(Y); %进行奇异值分解
Ysv = Y*V'*Dk;
p=0.001;
yita=chi2inv(1-p,Na^2);
Sumvector=ones(length(Searching_doa),1);
R=X*X'/snapshot;
[EDV,ED]= eig(R);
EVAq=diag(ED)'; %对角矩阵重拍
[EVA,I]=sort(EVAq); %特征值排序
EVA=fliplr(EVA); %特征值反褶
P_esv=(norm(EVA(:,(3:end))))^2;
cvx_begin quiet %CVX 工具包
variables p q
variables r(length(Searching_doa)) % 表示决策向量是一个 1801 维的向量
variable SSV1(length(Searching_doa),K) complex; % 表示决策向量是一个 1801*2 的复数矩阵
expression xsv(length(Searching_doa),1)
expressions Zk(Na,K) complex
minimize(p+5*q); %合理选择正则化参数
subject to
Zk = Ysv-AA*SSV1;
Zvec = vec(Zk); %把矩阵转化为向量
norm(Zvec) <=p ; %第一个不等式约束
Sumvector'*r<=q; %第二个不等式约束
for i=1:length(Searching_doa) %第三个不等式约束
xsv(i,:)=norm(SSV1(i,:));
end
for i=1:length(Searching_doa)
xsv(i)<=r(i);
end
cvx_end
power=10*log10(abs(xsv)/max(abs(xsv)));
figure()
plot(Searching_doa,power,'r');
xlabel('DOA/degree');
ylabel('PowerdB');
clear all;
close all;
clc;
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 2022 年 10 月 7 日
%% question three
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 系统参数
c = 3e8; %光速
Ts = 1.25e-7; %采样周期
fs = 1/Ts; %采样频率(8M)
T = 3.2e-5; %chirp 周期
Nf = 32; %一帧有 32 个 chirp
L = 0.0815; %每个虚拟孔径的长度
gama = 78.986e12; %调频率
Na = 86; %阵元个数
f0 = 78.8e9; %中心频率
POINT_NUM = 256; %点数
lmda = c/f0; %波长
B = gama*T; %chirp 带宽
dd = 2*L/(Na-1); %阵元间距
%% 导入数据
load('data_q3.mat');
b_3=permute(Z_time,[2 3 1]);
for i = 1:32
%% 1.基线法测距
R0_x = (0:fs/(POINT_NUM-1):fs)*c/(2*gama); %距离维度坐标
theta_y=-90:180/(128-1):90; %角度维度坐标
mm =abs(fftshift((fft((fft(b_3(:,:,i),[],2)),128,1)),1)); %基线法
win = hann(length(mm(1,:)));
win = repmat(win,1,128).';
mm_hanming = mm.*win;
figure((i-1)*2+1);
mesh(R0_x,theta_y,mm_hanming); %画出 R-thita 图
axis([0 10 -90 90])
%% 2.SRT-MUSIC 在线测角
b_4=b_3(:,:,i);
thita = 0:0.001:180; %角度搜索范围
d = 0:dd:(Na-1)*dd;
Z=b_4;
R=Z*Z'/POINT_NUM; %信号的自相关函数
[EV,D]=eig(R); %相关函数特征值分解
EVAq=diag(D)'; %对角矩阵重拍
[EVA,I]=sort(EVAq); %特征值排序
EVA=fliplr(EVA); %特征值反褶
EV=fliplr(EV(:,I)); %特征向量反褶
G = EV(:,3:end); %提取噪声子空间
G_rank=rank(G);
G_2=G(83:end,:);
G_2ni=pinv(G_2);
G_s=G*G_2ni;
G_3=G(1:82,:)*G_2ni;
for ii=1:length(thita) %谱峰搜索
A=exp(1i*2*pi*d/lmda*cos(thita(ii)*pi/180)).';
A_1=A(1:82,:);
A_2=A(83:end,:);
S(ii)=1/((A_1'*G_3*G_3'*A_1)+37+2*real(A_1'*G_3*A_2));
end
figure((i-1)*2+2);
plot(thita-90,20*log10(abs(S)/max(abs(S))),'k');hold on; %将谱峰功率转换成 dB
grid on;hold on;
title('SRT-MUSIC 测角')
xlabel('目标方位(度)')
ylabel('输出功率(dB)')
end
clc
clear all
close all
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 2022 年 10 月 9 日
%% question four
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 系统参数
c = 3e8; %光速
Ts = 1.25e-7; %采样周期
fs = 1/Ts; %采样频率(8M)
T = 3.2e-5; %chirp 周期
Nf = 32; %一帧有 32 个 chirp
L = 0.0815; %每个虚拟孔径的长度
gama = 78.986e12; %调频率
Na = 86; %阵元个数
f0 = 78.8e9; %中心频率
POINT_NUM = 256; %点数
lmda = c/f0; %波长
B = gama*T; %chirp 带宽
dd = 2*L/(Na-1); %阵元间距
derad = pi/180; %deg -> rad
radeg = 180/pi;
twpi = 2*pi;
kelm = Na; %阵列数量
dd = 0.5; %space
iwave = 2; %源个数
%% 导入数据
load('data_q4.mat');
Z = Z_antnoisy;
chose = [0,1] %选择想运行的算法
%% 1.联合相位误差自适应预校正和 MUSIC 的 DOA 估计算法
if (chose(1))
kk = angle(Z);
for i = 1: 85
phy_cha(i,:) = kk(i+1,:)- kk(i,:);
end
figure(1);
mesh(phy_cha);
gamma = 50;
for i = 1:256
mean_phy = mean(phy_cha(:,i));
for j =1:85
if( abs(phy_cha(j,i)) > gamma * mean_phy )
if(phy_cha(j,i)>0)
Z(j+1,i) = Z(j+1,i)*exp(1i*(-phy_cha(j,i)));
phy_cha(j,i) = angle(Z(j+1,i))-angle(Z(j,i));
if(j<85)
phy_cha(j+1,i) = angle(Z(j+2,i))-angle(Z(j+1,i));
end
else
Z(j+1,i) = Z(j+1,i).*exp(1i*(-phy_cha(j,i)));
phy_cha(j,i) = angle(Z(j+1,i))-angle(Z(j,i));
if(j<85)
phy_cha(j+1,i) = angle(Z(j+2,i))-angle(Z(j+1,i));
end
end
end
end
end
kk1 = angle(Z);
for i = 1: 85
phy_cha1(i,:) = kk1(i+1,:)- kk1(i,:);
end
figure(2);
mesh(phy_cha1);
R0_x = (0:fs/(512-1):fs)*c/(2*gama); %距离维度坐标
theta_y=-90:180/(256-1):90; %角度维度坐标
mm =abs(fftshift((fft((fft(Z,512,2)),512,1)),1)); %基线法
mm1 = fft(Z,[],2);
mesh(abs(mm1));
mesh(abs(mm));
imagesc(R0_x,theta_y,mm);
imagesc(abs(mm1))
Rxx=Z*Z'/POINT_NUM;
[EVq,D]=eig(Rxx);%%%%
EVA=diag(D)';
[EVA,I]=sort(EVA);
EVA=fliplr(EVA);
EV=fliplr(EVq(:,I));
d=0:dd:(kelm-1)*dd; %
iang = -90:0.0001:90;
for kk = 1:length(iang)
a=exp(-1i*twpi*d*sin(derad*iang(kk))).';
En=EV(:,2+1:kelm);
SP(kk)=1/(a'*En*En'*a);
end
figure(3);
SP=abs(SP);
SPmax=max(SP);
SP=10*log10(SP/SPmax);
h=plot(iang,SP);
set(h,'Linewidth',2)
xlabel('angle (degree)')
ylabel('magnitude (dB)')
%
set(gca, 'XTick',[-90:10:90])
grid on
out=Peak_Seek(iang,SP,2);
end
%% 2.基于特征空间的幅相误差和角度联合迭代优化方法
if(chose(2))
Rxx=Z*Z'/POINT_NUM;
% InvS=inv(Rxx); %%%%
[EVq,D]=eig(Rxx);%%%%
EVA=diag(D)';
[EVA,I]=sort(EVA);
EVA=fliplr(EVA);
EV=fliplr(EVq(:,I));
d=0:dd:(kelm-1)*dd;
iang = -90:0.001:90;
for kk = 1:length(iang)
a=exp(-j*twpi*d*sin(derad*iang(kk))).';
En=EV(:,2+1:kelm);
% SP(kk)=(a'*a)/(a'*En*En'*a);
SP(kk)=1/(a'*En*En'*a);
end
%
figure(1);
SP=abs(SP);
SPmax=max(SP);
SP=10*log10(SP/SPmax);
h=plot(iang,SP);
set(h,'Linewidth',2)
xlabel('angle (degree)')
ylabel('magnitude (dB)')
set(gca, 'XTick',[-90:10:90])
grid on
out=Peak_Seek(iang,SP,iwave);
w=[1;zeros(kelm-1,1)];
% [temp,i0]=min(abs(theta-mean(sita0)));
Tao=diag([1;randn(kelm-1,1)+j*randn(kelm-1,1)]);
Tao=diag(ones(kelm,1));
% ==== ==== 通道幅相误差的自校正算法
for num=1:100
clear SP est_cita
num
% ==== 搜索 P 个角度
for ii=1:length(iang)
% a_theta=exp(j*2*pi/lamda*r*cos(theta(ii)-2*pi*k/M)*cos(fai0(1)));
a_theta=exp(-j*twpi*d*sin(derad*iang(ii))).';
% SP(ii)=1/sum((abs((Tao*a_theta)'*En).^2));
% SP(ii)=(a_theta'*a_theta)/(a_theta'*En*En'*a_theta);
SP(ii)=1/((Tao*a_theta)'*En*En'*(Tao*a_theta));
end
figure(3);plot(iang,10*log10(SP/max(SP)));pause(2);hold on;
% i1=find(Pc(1:i0)==max(Pc(1:i0)));i2=find(Pc(i0:end)==max(Pc(i0:end)));
out(num+1,:)=Peak_Seek(iang,SP,iwave);
if(out(num+1,1)>0.3&&out(num+1,1)<-0.3) out(num+1,1)=out(num,1); end
if(out(num+1,2)>0.3&&out(num+1,2)<-0.3) out(num+1,2)=out(num,2); end
% est_cita=[theta(i1) theta(i0+i2-1)];EST_cita(num,:)=est_cita/pi*180;
clear Tao gama
Q=zeros(kelm,kelm);
for jj=1:iwave
% a_cita=exp(j*2*pi/lamda*r*cos(est_cita(jj)-2*pi*k/M)*cos(fai0(1)));
a_cita=exp(-j*twpi*d*sin(derad*out(num+1,jj))).';
erfa=diag(a_cita);
Q=Q+erfa'*En*En'*erfa;
end
gama=inv(Q)*w/(w.'*inv(Q)*w);
Tao=diag(gama);
J(num)=gama'*Q*gama;
if num>=2 & (abs(J(num-1)-J(num))<2e-3)
break
end
end
end