2023.9.12

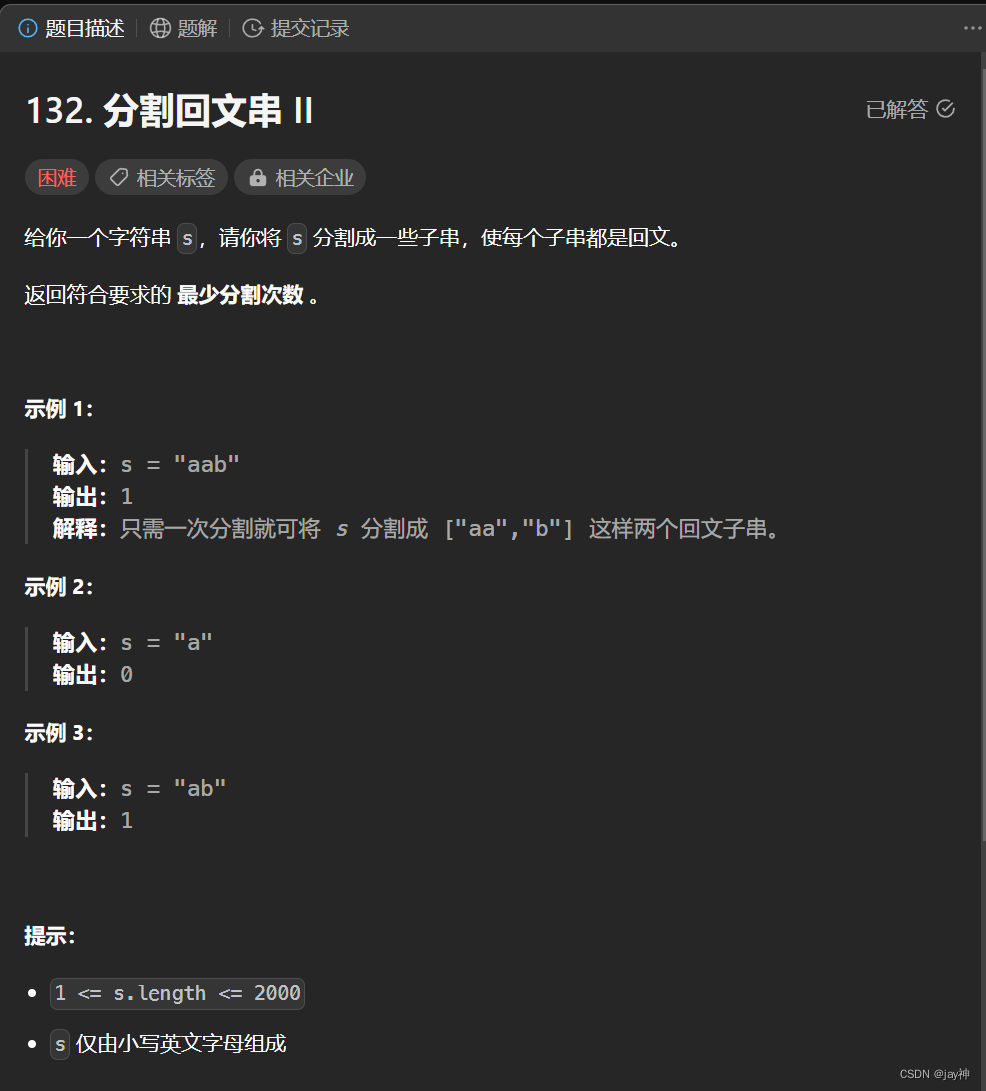
         dp算法经典题之回文子串，先联想到 回文子串。 先用传统回文子串的dp方法定义一个二维数组存储该字符串的各子串是否为回文子串。 再定义一个一维dp数组用于存储下标0~i的最小分割次数。  

        初始化：先将该dp数组初始化为最坏情况，即下标0为0，下标1为1。(意思就是一个字符要分割0次，两个字符要分割1次)。

        遍历：核心递推公式为：dp[i] = min(dp[i] , dp[j]+1);  

        直接看代码：

class Solution {
public:
    int minCut(string s) {
        //回文子串经典代码：定义一个二维数组存储子串是否为回文。
        vector<vector<bool>> is_backstr(s.size(),vector<bool>(s.size(),false));
        for(int i=s.size()-1; i>=0; i--)
        {
            for(int j=i; j<s.size(); j++)
            {
                if(s[i] == s[j])
                {
                    if(j - i <= 1) is_backstr[i][j] = true;
                    else is_backstr[i][j] = is_backstr[i+1][j-1];
                }
            }
        }
        //定义dp数组，dp[i]代表下标0~i的最小分割次数
        vector<int> dp(s.size());
        //初始化。 即最少分割次数的最坏情况
        for(int i=0; i<s.size(); i++)
        {
            dp[i] = i;
        }
        //遍历
        for(int i=1; i<s.size(); i++)
        {
            if(is_backstr[0][i]) dp[i] = 0; //已经是回文串了，最小分割次数为0
            for(int j=0; j<i; j++)
            {
                if(is_backstr[j+1][i])
                {
                    dp[i] = min(dp[i] , dp[j]+1);
                }
            }
        }
        return dp[s.size()-1];
    }
};