我是目录
- 0. 前言
- 1. Fibonacci Heap介绍
- 1.1 简单回顾堆和优先队列
- 1.2 二项树
- 1.3 二项堆
- 2. 那怎么推导出Fibonacci Heap?
- 2.1 实现GetMin
- 2.2 实现Insert
- 2.3 实现ExtractMin
- 2.4 实现DecreaseKey
- 2.5 关键部分
- 3. 那么,和斐波那契数列有什么关系?
- 4. Java实现
- 4.1 核心数据结构定义
- 4.2 ExtractMin实现
- 4.3 DecreaseKey实现
- 4.4 Consolidate实现
- 4.5 完整代码
- 4.6 都看到这里了,不妨点个赞再走吧!
- 4.7 后记
- 5. 参考
0. 前言
在一个项目中用到了DJ特斯拉,不是,Dijstra算法,对一个很大的图找某个节点间的最短路,找了一些加速的方法,其中提到了斐波那契堆(Fibonacci Heap),让我来康康这是何方神圣。
1. Fibonacci Heap介绍
1.1 简单回顾堆和优先队列
在我们日常学习和工作中,接触到的堆Heap一般指二叉堆,Binary Heap,即由完全二叉树来实现的堆,一般最小堆用的比较多,即从根节点开始,子节点的值都比根节点小。如果要用大根堆,只需在添加元素时对元素取反即可,在取出时也取反就能获得想要的元素。通常用数组结构来实现。
优先队列(Priority Queue)是一种常见的数据结构,顾名思义,它与普通队列不同在于它不是先进先出的,而是给其中每个元素都关联一个优先级(or权重),优先级高的元素先出。
二者关系:优先队列是一种数据结构的抽象概念,并没有规定具体的实现方式,只要满足优先级的要求即可。二叉树的特点使得其非常合适用来实现优先队列,例如Java中的java.util.PriorityQueue类就是用二叉堆来实现的。
1.2 二项树
二叉堆使用数组来存放节点,于是对于一个很大的堆,当二叉树的深度较深时,某个节点的子节点就可能跟它不在同一个内存页了,极端情况下如果恰好子节点在三级缓存中都缺失,就得去内存中找,那就带来了访存的开销。其次,在合并两个二叉堆时,效率也很低,因为需要开辟新的内存空间,将两个堆中的元素放入新内存,重新调整堆结构。
为了解决二叉堆的这两个问题,引入二项堆,Binomial Heap。它是一种类似于二叉堆的堆结构。与二叉堆相比,其优势是可以快速合并两个堆,因此它属于可合并堆(mergeable heap)抽象数据类型的一种。
二项树是递归定义的:
- 度数为0的二项树只包含一个节点
- 度数为k的二项树有一个根节点,根节点下有k个子树(子节点),每个节点分别是度数分别为k-1, k-2, …,2,1,0的二项树。

度数为k的二项树可以很容易从两颗度数为k-1的二项树合并得到:把一颗度数为k-1的二项树作为另一颗原度数为k-1的二项树的最左子树。这一性质是二项堆用于堆合并的基础。
1.3 二项堆
二项堆是指满足以下性质的二项树的集合:
- 每棵二项树都满足最小堆性质,即节点关键字大于等于其父节点的值
- 不能有两棵或以上的二项树有相同度数(包括度数为0)。换句话说,具有度数k的二项树有0个或1个
第一个性质保证了二项树的根节点包含了最小的关键字。第二个性质则说明节点数为n的二项堆最多只有log n棵二项树。实际上,包含n个节点的二项堆的构成情况,由n的二进制表示唯一确定,其中每一位对应于一颗二项树。例如,13的二进制表示为1101,所以有13个节点的二项堆由度数为3, 2, 0的三棵二项树组成:

因为我们并不需要对二项树的根节点进行随机存取,我们只关心我们想要的最小值(最大值)是什么,所以我们可以用一个双向链表来存储这些二项树的根节点,链表的起点就是我们想要的最小值节点。
2. 那怎么推导出Fibonacci Heap?
我们知道二叉堆的特地是它的四种操作和复杂度分别是:
- GetMin: O(1)
- Insert: O(log n)
- ExtractMin: O(log n)
- DecreaseKey: O(log n)
DecreaseKey指减小某节点的值,然后要调整堆结构。
现在我们想要一个更快的数据结构,它能让我们很懒的在**O(1)时间内插入一个新元素,在O(1)**时间内减少一个节点的值并调整堆结构。

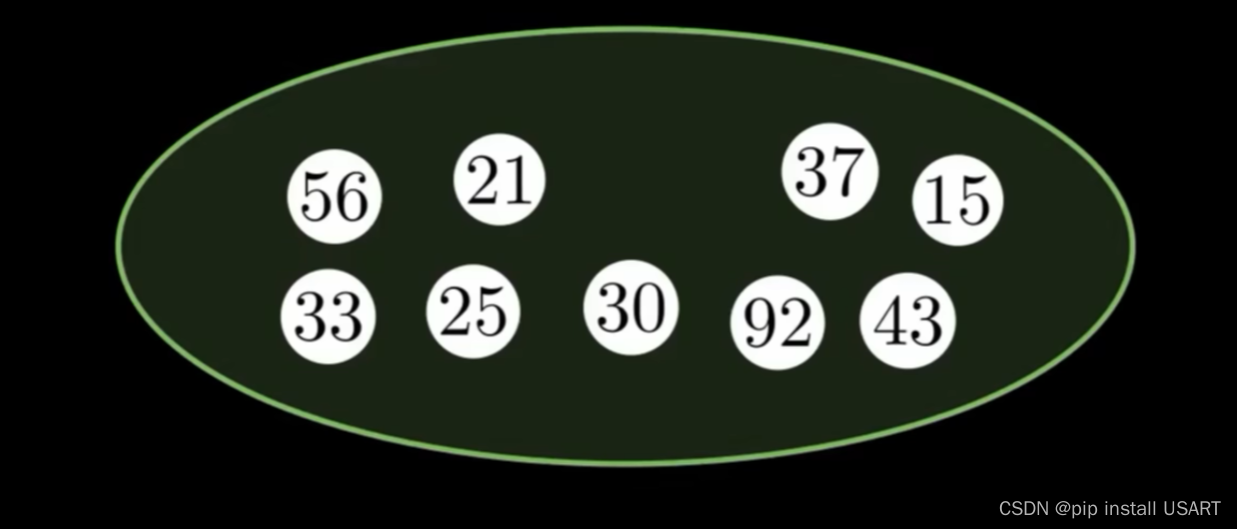
插入15,比21小,直接把指针移过去。

把78改成12,直接访问78,改了之后把最小值指针移过去。

把12踢出去,再快速找到15。
改进前面提到的二项堆,将子节点之间也用双向链表连接起来,同时记录每个节点的父子节点。
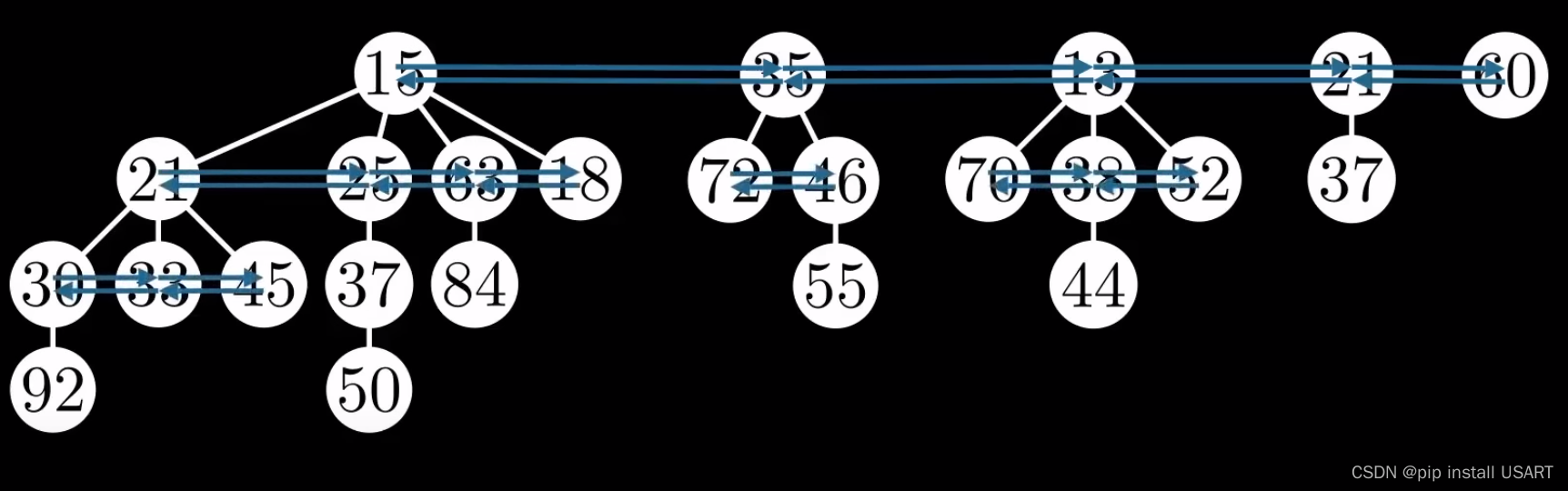
最小值永远会在根节点链表上,只需要一个指针指向它,我们就能访问整个堆。假如要把最小值13踢掉,谁是下一个最小值?根据堆的特点,要么会是其他根节点中的某个,要么就是13的子节点中的某个。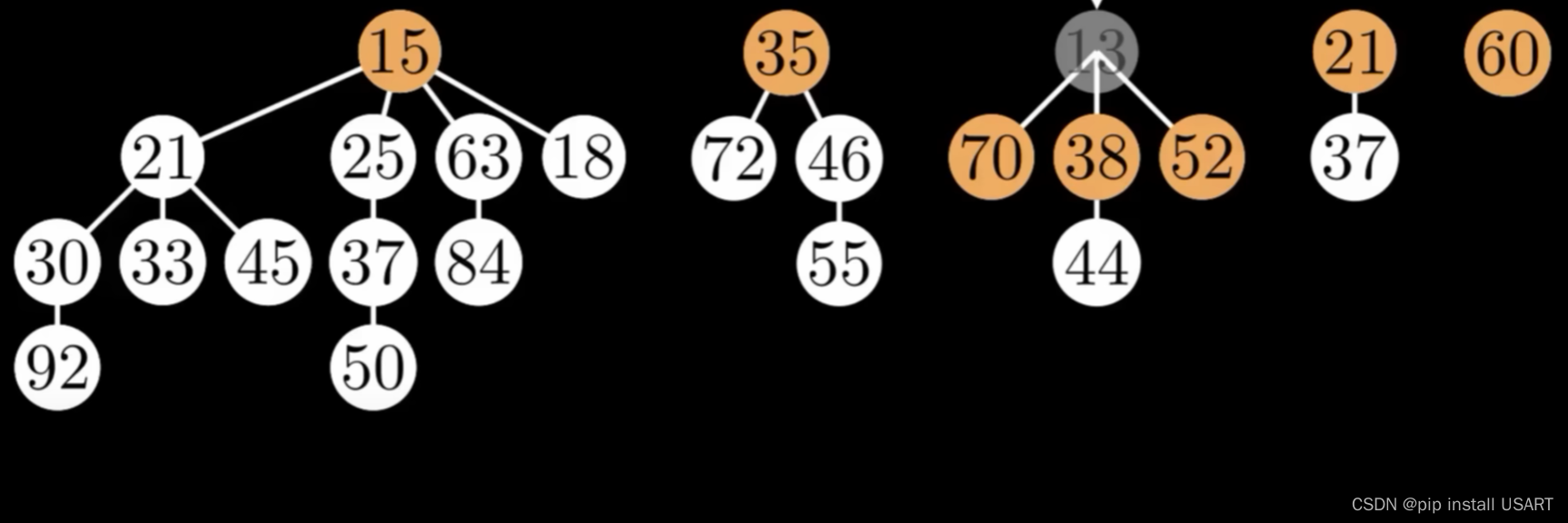
2.1 实现GetMin
现在已经实现了O(1)的GetMin,那Insert怎么说?
2.2 实现Insert
没错,最简单的就是直接插入一个度为0的新根节点,然后再更新最小值指针。
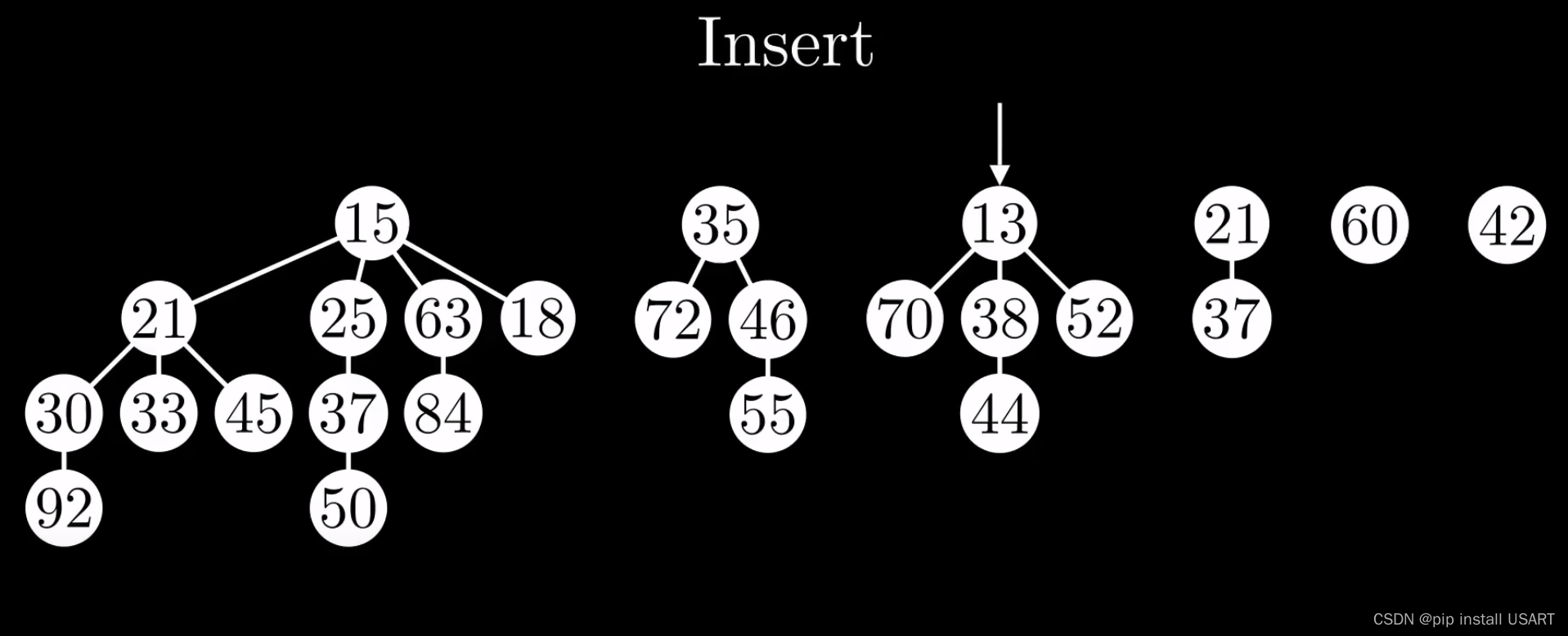
但是也不能一直插入一个单节点,那样不就成了一个链表了?那GetMin不就O(N)了?理想的,对很多新插入的节点,把节点往一棵树上或者多棵树上怼不就完事儿了,同时记住树的数量要尽可能少。
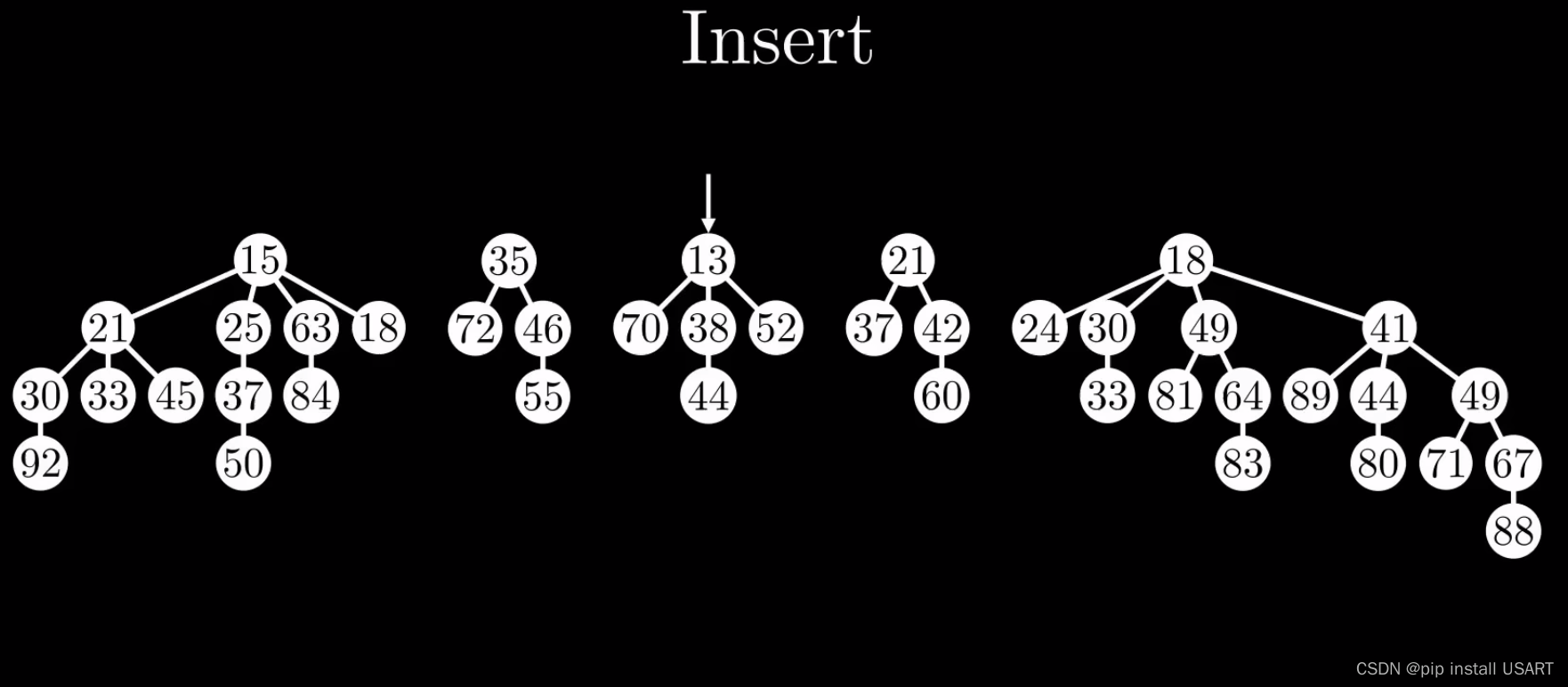
一直插入一个单节点,导致ExtractMin变成O(N)。渐进的来看,每次插入一个节点多做一步操作,那ExtractMin的N复杂度不就可以被分摊到1了?
2.3 实现ExtractMin
1.首先踢出最小值,如果它有子节点,那就把所有子节点作为独立的树插入到根链表中。
2.清理现场,维护堆特性。要让树尽可能的少,需要对树进行合并。合并时,把根节点值大的那棵树作为子节点合并到较小的那一棵上。
 |  |
需要树尽可能的少,于是用一个数组来记录根节点的度数情况,遍历所有树,对两个度数为k的树,合并为一棵度数为k+1的树,如果度数为k+1的树存在,继续该合并过程,直到所有度数只出现一次。
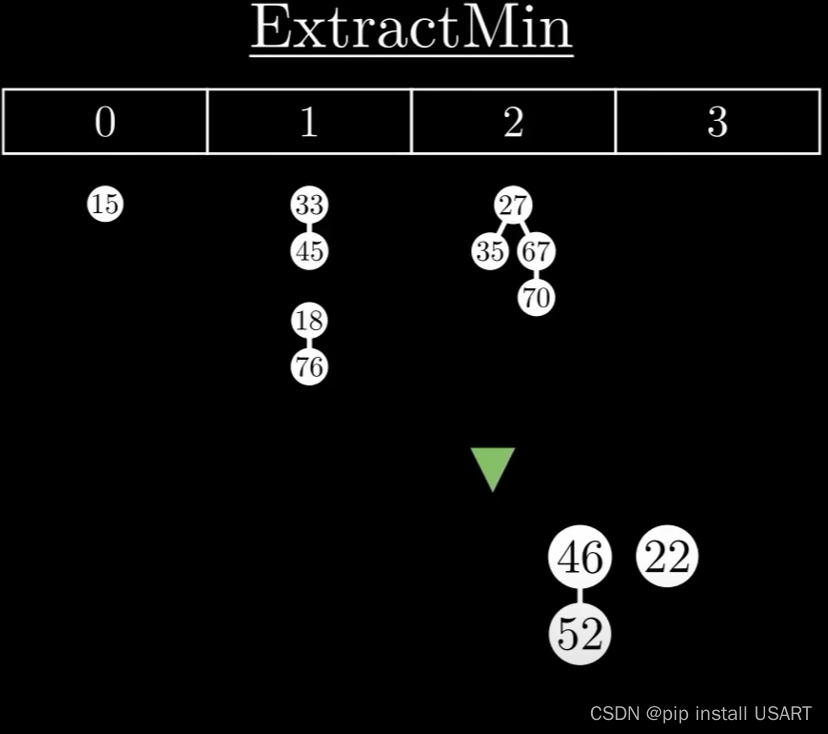
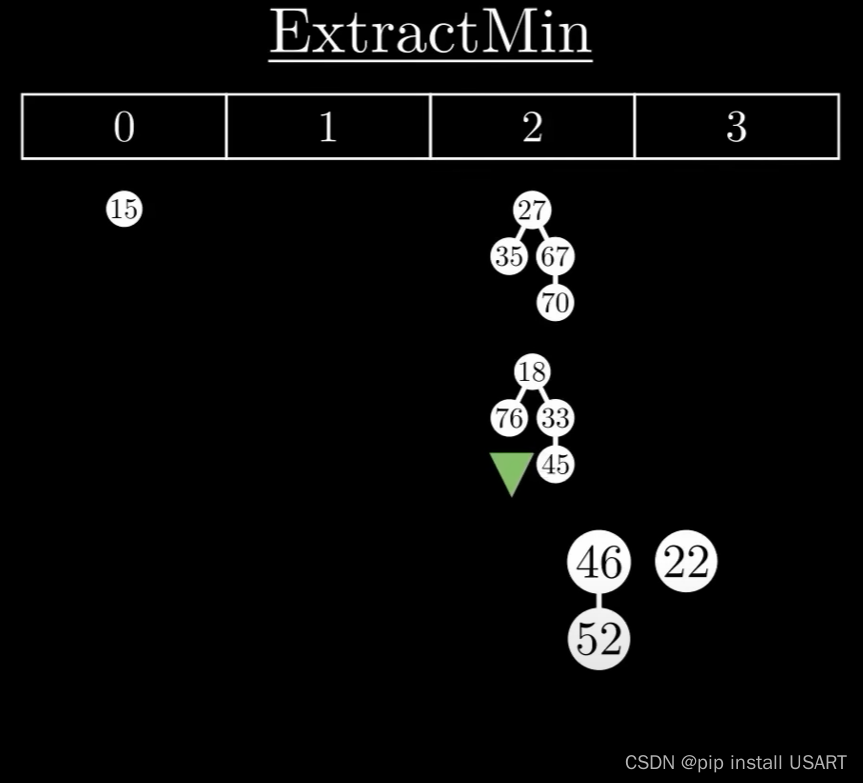
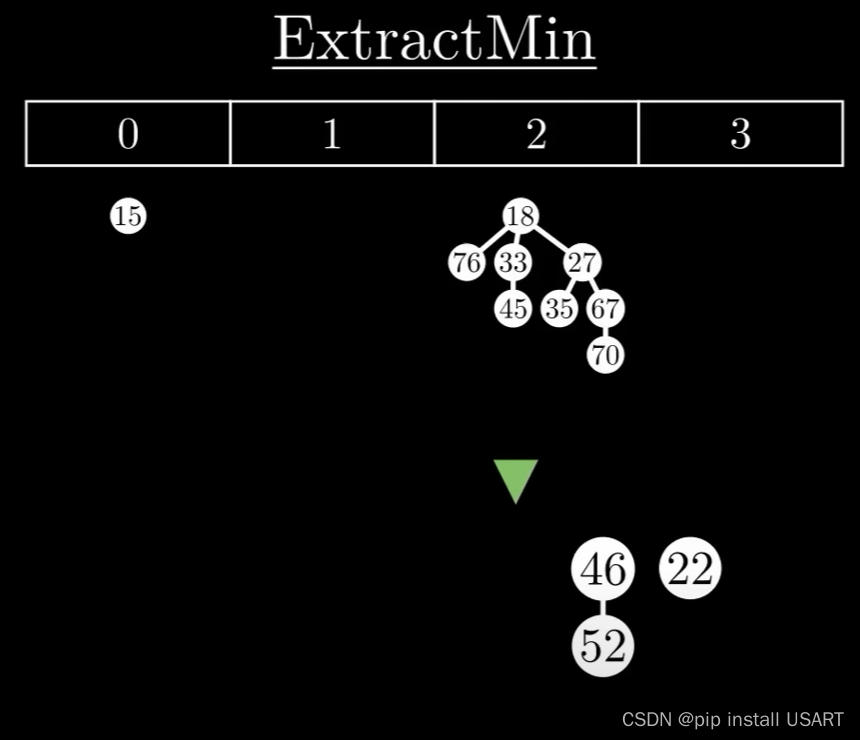
3.重建堆,再重新把这些根节点形成双链表,同时更新最小值指针。ExtractMin的时间复杂度与堆中最大树的度数有关,也就是max degree,而根据二项树的特性,max degree又和节点数目n成对数关系,即max degree = log(n)。所以ExtractMin的复杂度就是O(log n)。
2.4 实现DecreaseKey
假设下面这个堆,现在要对其中的62进行修改,如果修改后的值不违背堆的特性,那么就什么都不做,如果修改后的值比父节点小,说明违背了堆的特性,需要调整结构。如果还是用二叉树的自底向上冒泡进行调整父子节点,那时间复杂度还是O(log n),违背了斐波那契堆的初心。

所以,直接把这个节点给剪掉(cut),把它作为一个子树插入到堆中,同时更新最小值指针,那么这就只需要O(1)了。但是! 我要说但是了,回顾一下上面的ExtractMin,它的复杂度是与最大节点度数成对数关系,就是依赖于max degree对数级增长,而对数级增长的前提是堆中的树是二项树,如果对剪切节点不加以任何限制,那么树就不是二项树了,增长也变成了线性。

观察上面这个堆,可以按目前的方法调用十余次DecreaseKey将它们设为0并ExtractMin。
 现在这个树的度仍为4,但它只包含了5个节点。 于是,度为d的树的节点数从包含 2d变成了最少可以是d+1,进而最大节点度max degree不再是log(n),而是n-1,即线性了,导致ExtractMin就变成了O(N)的复杂度。那就带来了一个困境,如果不剪掉节点,那么DecreaseKey变慢、ExtractMin变快;如果剪掉节点,那么DecreaseKey变快、ExtractMin变慢。
现在这个树的度仍为4,但它只包含了5个节点。 于是,度为d的树的节点数从包含 2d变成了最少可以是d+1,进而最大节点度max degree不再是log(n),而是n-1,即线性了,导致ExtractMin就变成了O(N)的复杂度。那就带来了一个困境,如果不剪掉节点,那么DecreaseKey变慢、ExtractMin变快;如果剪掉节点,那么DecreaseKey变快、ExtractMin变慢。
2.5 关键部分
这就是斐波那契堆最关键的地方了。中庸之道——对每个节点,用一个变量对它进行标记,只允许它cut掉一个子节点,那么就能保留两个方法的优点,同时让ExtractMin变快,DecreaseKey变快。如果下次还是要cut掉该节点的一个子节点,那么就连带这个父节点一起剪掉,因为上一次剪切时已将它标记了,它已经失去了一个子节点。如下两图所示,将其中一个节点修改为19,cut后标记其父节点。
 | 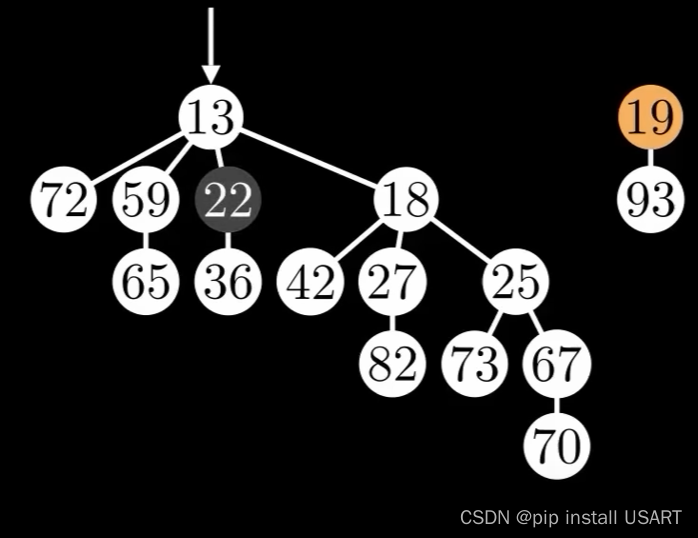 |
再修改22的子节点,变成16,此时因为22已经被标记,所以继续把它也剪掉。虽然这又违背了前面提到的树的数量尽可能少的原则,但是这是在满足度为k的树应该包含尽可能多的节点的前提下。在剪掉后,22不影响它的父节点,所以可以把它的标记恢复。
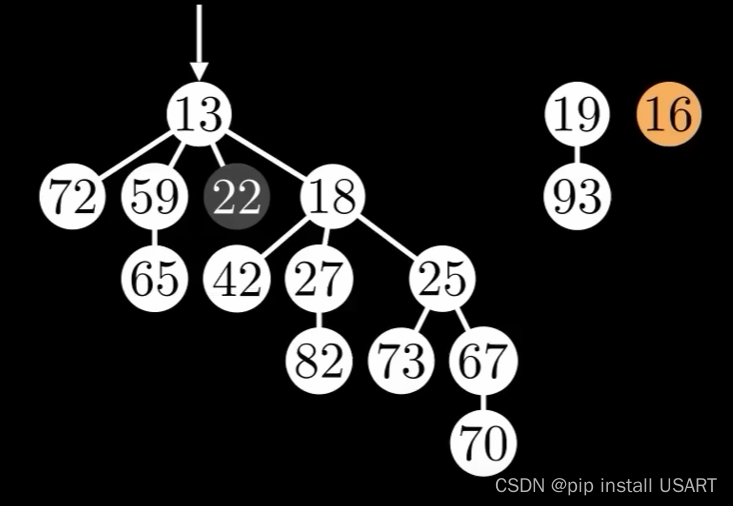 |  |
/**
* 剪枝
* @param x 子节点
* @param y x的父节点
*/
private void cut(FibNode x, FibNode y){
y.setDegree(y.getDegree() - 1);
// y度为0,则无子节点,设为null,否则应该设为x的右节点
y.setChild(y.getDegree() == 0 ? null : x.getRight());
// 独立出x
x.getRight().setLeft(x.getLeft());
x.getLeft().setRight(x.getRight());
x.setRight(null);
x.setLeft(null);
// 重新插入x
insert(x);
this.n--;
x.setParent(null);
x.setMark(false);
}
/**
* 级联剪枝y
* @param y 某父节点
*/
private void cascadingCut(FibNode y){
FibNode z = y.getParent();
if(z != null){
if(!y.getMark()){
y.setMark(true);
}
else{
cut(y, z);
cascadingCut(z);
}
}
}
3. 那么,和斐波那契数列有什么关系?
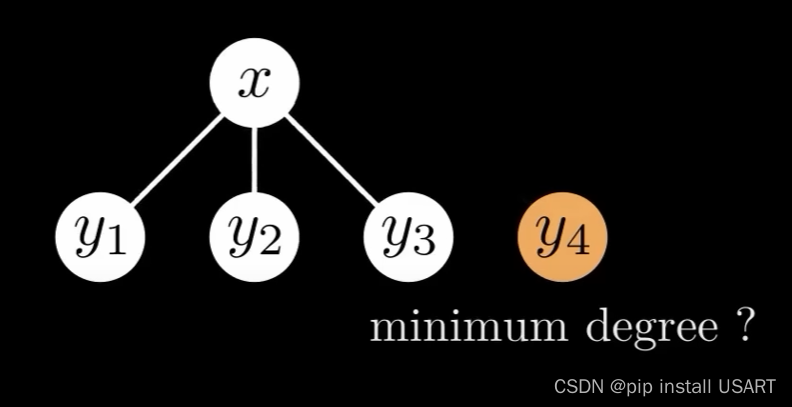
根据前面提到的规则,每次给一个节点添加子节点时是在其已有的子节点的右边,在合并两个树时,把根值大一点的作为子节点接到另一个节点的子节点右边,如下图所示,此时x的度为3,合并y4到给x意味着y4也是度至少为3,即至少有3个子节点。上面提到一个父节点第二次被cut掉一个子节点时自身也要被cut掉,于是y4必须至少还有两个子节点。那么,一个节点的第i个子节点的度至少要为i-2
 |  |
根据前面提到的所有规则,让我们开始构建一个斐波那契堆。
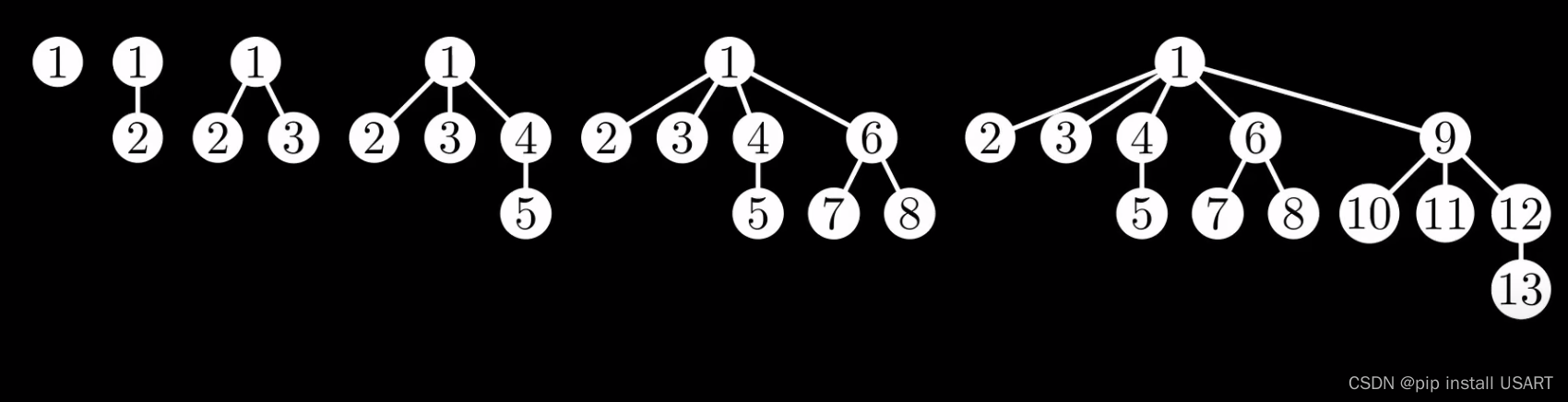
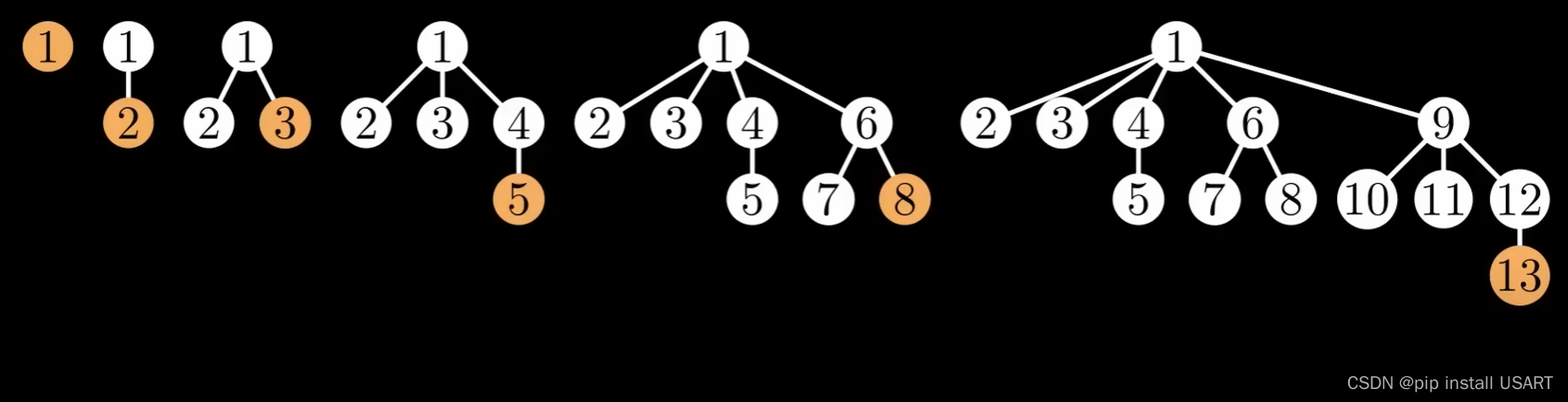
从左到右,每个树的根节点的度数依次为0,1,2,。。从中可以看出,第5棵树的第四4棵子树,和前面第3棵树的结构一样。这里就体现斐波那契数列了
4. Java实现
4.1 核心数据结构定义
class FibNode{
private FibNode parent;
private FibNode child;
private FibNode left;
private FibNode right;
private int degree;
private boolean mark;
private int key;
public FibNode(){
this.parent = null;
this.child = null;
this.left = this;
this.right = this;
this.degree = 0;
this.mark = false;
this.key = -1;
}
public FibNode(int key){
this();
this.key = key;
}
// Setters and Getters
void setParent(FibNode parent){
this.parent = parent;
}
FibNode getParent(){
return this.parent;
}
void setChild(FibNode child){
this.child = child;
}
FibNode getChild(){
return this.child;
}
void setLeft(FibNode left){
this.left = left;
}
FibNode getLeft(){
return this.left;
}
FibNode getRight(){
return this.right;
}
void setRight(FibNode right){
this.right = right;
}
int getDegree(){
return this.degree;
}
void setDegree(int degree){
this.degree = degree;
}
boolean getMark(){
return this.mark;
}
void setMark(boolean mark){
this.mark = mark;
}
int getKey(){
return this.key;
}
void setKey(int key){
this.key = key;
}
}
4.2 ExtractMin实现
public int extractMin(){
FibNode z = this.min;
// min指针不为空,堆中有元素
if(z != null){
// 获取堆顶的子节点,把所有子节点重新插入到堆中
FibNode c = z.getChild();
FibNode k = c, temp;
if(c != null){
do{
temp = c.getRight();
insert(c);
// insert内部会把n+1,此处调节结构,不是真的加节点,所以n--
this.n--;
c.setParent(null);
c = temp;
}while(c != null && c != k);
}
// 放出根节点
z.getLeft().setRight(z.getRight());
z.getRight().setLeft(z.getLeft());
z.setChild(null);
// 放出后z还等于z的right,说明根节点时唯一的节点
if(z == z.getRight()){
this.min = null;
}
else{
this.min = z.getRight();
// 调整堆结构
this.consolidate();
}
this.n--;
z.setLeft(null);
z.setRight(null);
return z.getKey();
}
// 堆为空,返回一个int类型最大值
else{
return Integer.MAX_VALUE;
}
}
4.3 DecreaseKey实现
private void decreaseKey(FibNode x, int k){
// 新值比原值大,忽略这个操作
if (k > x.getKey()){
return;
}
x.setKey(k);
FibNode y = x.getParent();
if(y != null && x.getKey() < y.getKey()){
// 设置新值后,子节点值可能比父节点大,违反堆的性质,进行剪枝
cut(x, y);
// 级联剪枝y
cascadingCut(y);
}
if(x.getKey() < this.min.getKey()){
this.min = x;
}
}
4.4 Consolidate实现
public void consolidate(){
int Dofn = (int) (Math.log(this.n) / Math.log(PHI));
// int Dofn = this.n; // 或者this.n,只不过更浪费空间
// 记录二项树度数的数组
FibNode[] A = new FibNode[Dofn + 1];
for(int i = 0; i <= Dofn; i++){
A[i] = null;
}
FibNode w = this.min;
if(w != null){
// 标记遍历根节点是否结束
FibNode check = this.min;
do{
FibNode x = w;
int d = x.getDegree();
while(A[d] != null && A[d] != x){
FibNode y = A[d];
// 保证y指向的节点值比x的大
if(x.getKey() > y.getKey()){
FibNode temp = x;
x = y;
y = temp;
w = x;
}
// 把y接到x下面
FibHeapLink(y, x);
check = x;
A[d] = null;
d++;
}
A[d] = x;
w = w.getRight();
}while(w != null && w != check);
// 先置空根节点,重新插入堆中
this.min = null;
for(int i = 0; i <= Dofn; ++i){
if(A[i] != null){
insert(A[i]);
this.n--;
}
}
}
}
4.5 完整代码
github地址
4.6 都看到这里了,不妨点个赞再走吧!
4.7 后记
其实一般用二叉堆实现的优先队列就够了,使用这个堆去优化DJ特斯拉,不是,Dijkstra只适用于场景非常大的情况下,首先图中的边与节点的数量关系至少要是n~e2,其次具体的加速效果还与实现代码的运行效率有关,低效的代码反而容易拖慢节奏,以上代码仅供参考,实际请以具体场景为准。
5. 参考
Fibonacci Heaps or “How to invent an extremely clever data structure”
https://www.programiz.com/dsa/fibonacci-heap
二项树和二项堆-维基百科