第一章 神经网络是如何实现的

上节描述的网络结构比较特殊，不具有一般性。比如前面我们讲过的权重都是1或者-1，这是很特殊的情况，实际上权重可以是任何数值，可以是正的，也可以是负的，也可以是带小数的。权重的大小可以体现模式在不同位置的重要程度。比如，在笔画的中心位置，权重可能会比较大，而在边缘可能会比较小。这些权重也不是依靠手工设置的，而是通过样例学习到的。

那么神经网络是如何学习的呢？此节会先给出神经元和神经网络的一般性描述，然后下节会描述如何训练神经网络。

二、神经元与神经网络

• 神经元和神经网络，指的是人工神经元和人工神经网络，为了简化起见，我们常常省略“人工”二字。

1. 神经元

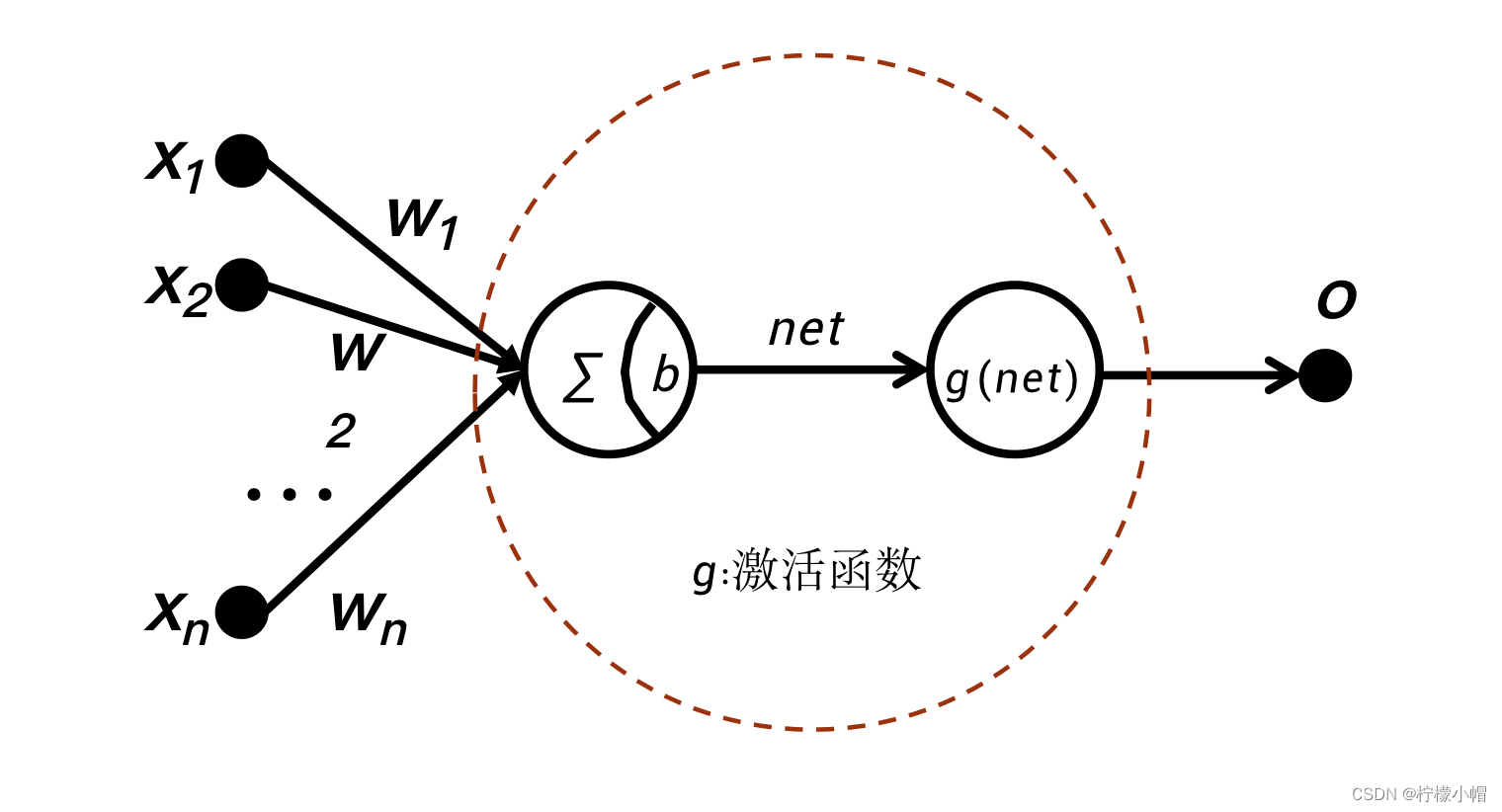
• 什么是神经元呢？图示的就是一个神经元，它有$x_1$、$x_2$ … $x_n$ 共n个输入，每个输入对应一个权重$w_1$、$w_2$、… 、$w_n$，一个神经元还有一个偏置b，每个输入乘以对应的权重并求和，再加上偏置b，我们用net表示：
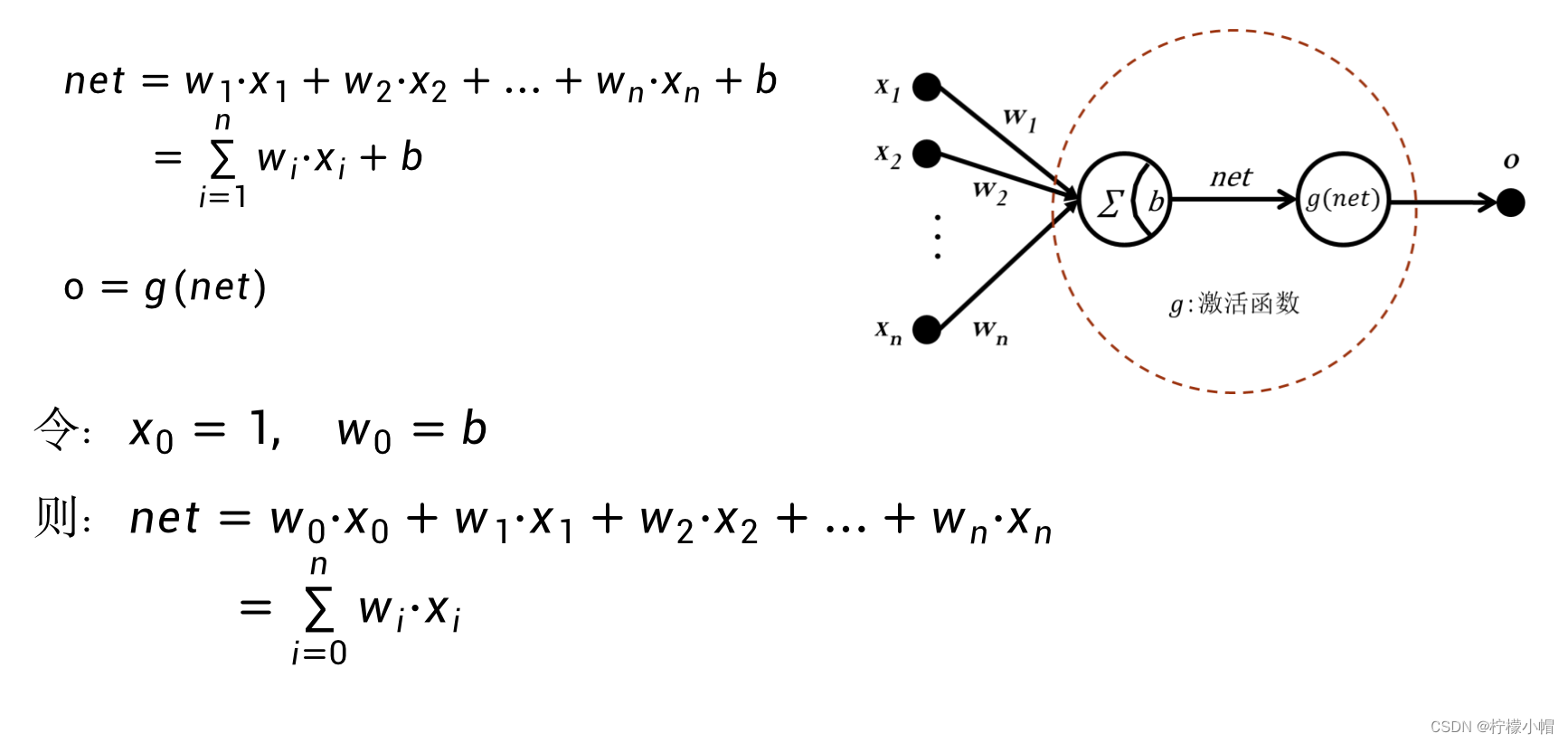
  $$net=w_1\cdot x_1+w_2\cdot x_2+\cdots +w_n\cdot x_n+b=b+\sum _{i=1}^n{w}_i\cdot x_i$$
• 对net再施加一个函数g，就得到了神经元的输出o：
  $$o=g(net)$$
• 这就是神经元的一般描述。为了更方便地描述神经元，我们引入$x_0=1$，并令$w_0=b$，则net也可以表示为：
  $$net=w_0\cdot x_0+w_1\cdot x_1+w_2\cdot x_2+\cdots +w_n\cdot x_n=\sum _{i=0}^n{w}_i\cdot x_i$$
  

2. 神经元的向量表示

• 为了表达简便，要引入向量的概念。
• 可以把n个输入$x_i$ 用一个向量$x$ 表示：$x=[x_0,x_1,\cdots ,x_n]$ ，同样，权重也可以表示为向量：$w=[w_0,w_1,\cdots ,w_n]$ ，这样net就可以表示为两个向量的点积：
  $$net=w\cdot x$$
• 向量的点积，就是两个向量对应元素相乘再求和。而神经元的输出o就可以表达为：
  $$o=g(net)=g(w\cdot x)$$
  
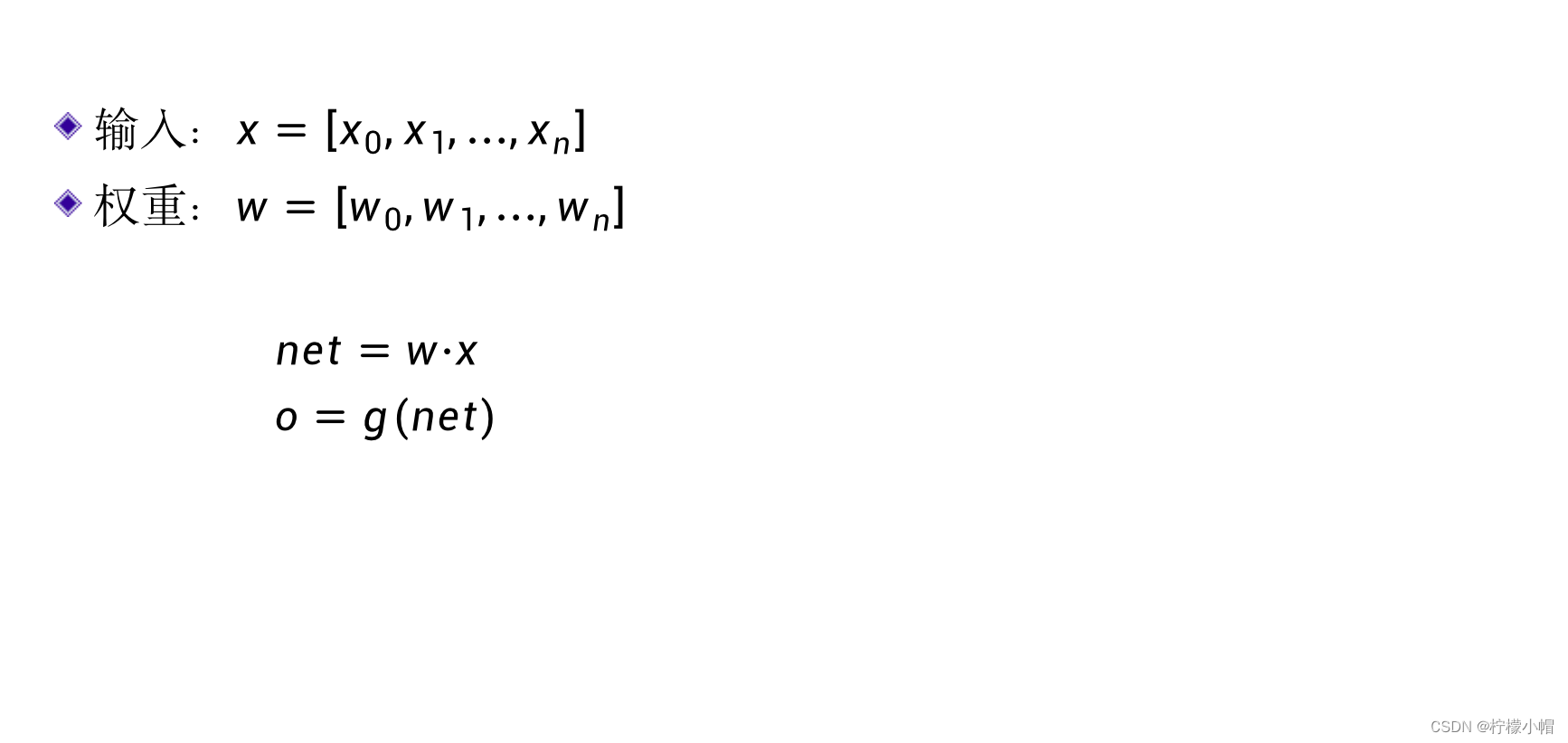
• $g$ 表示什么呢？

3. 激活函数

• 这里的 $g$ 叫激活函数。上节讲的sigmoid函数就是一个激活函数。除了sigmoid函数外，激活函数还可以有其他的形式。以下是常用的几种。

3.1 符号函数

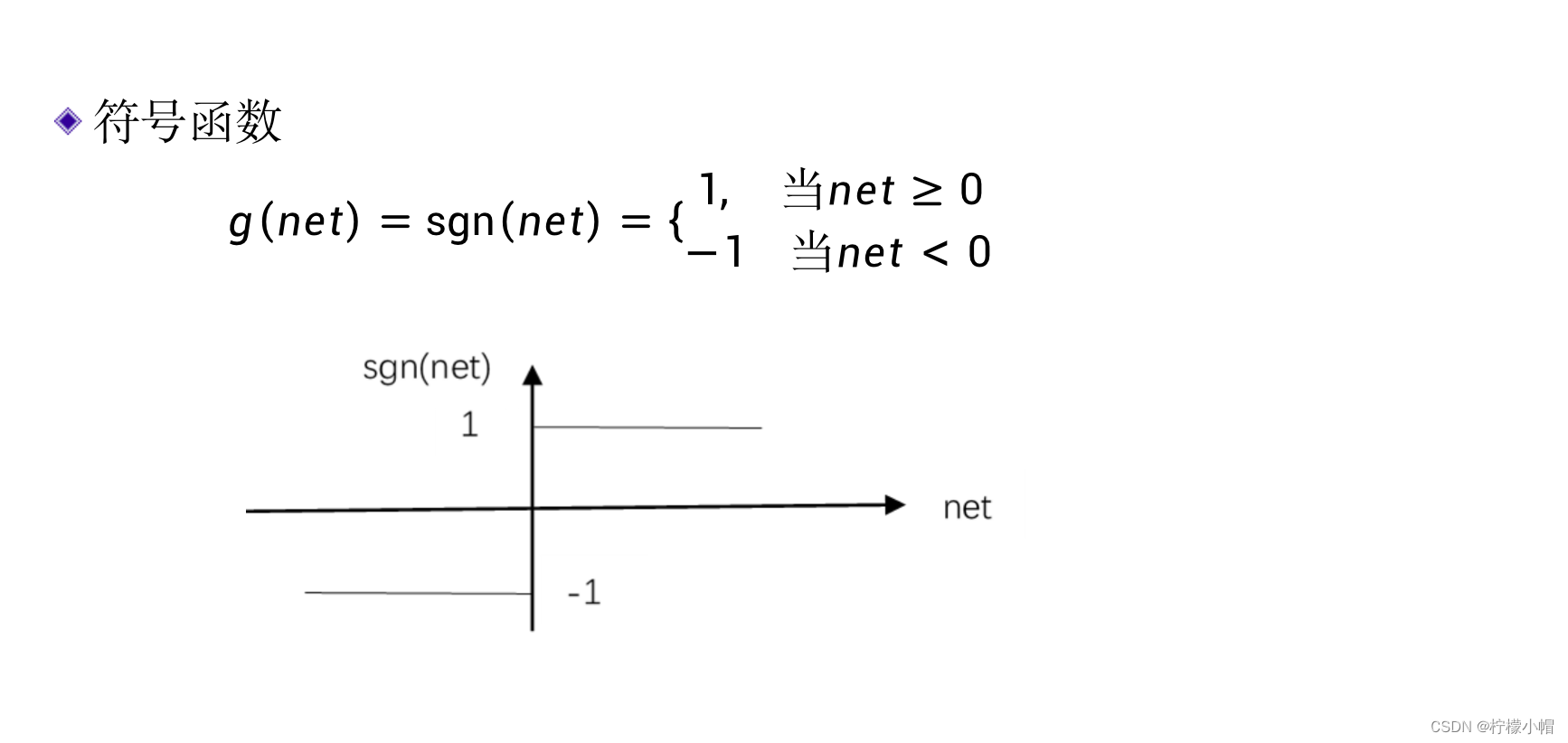
3.2 sigmoid函数

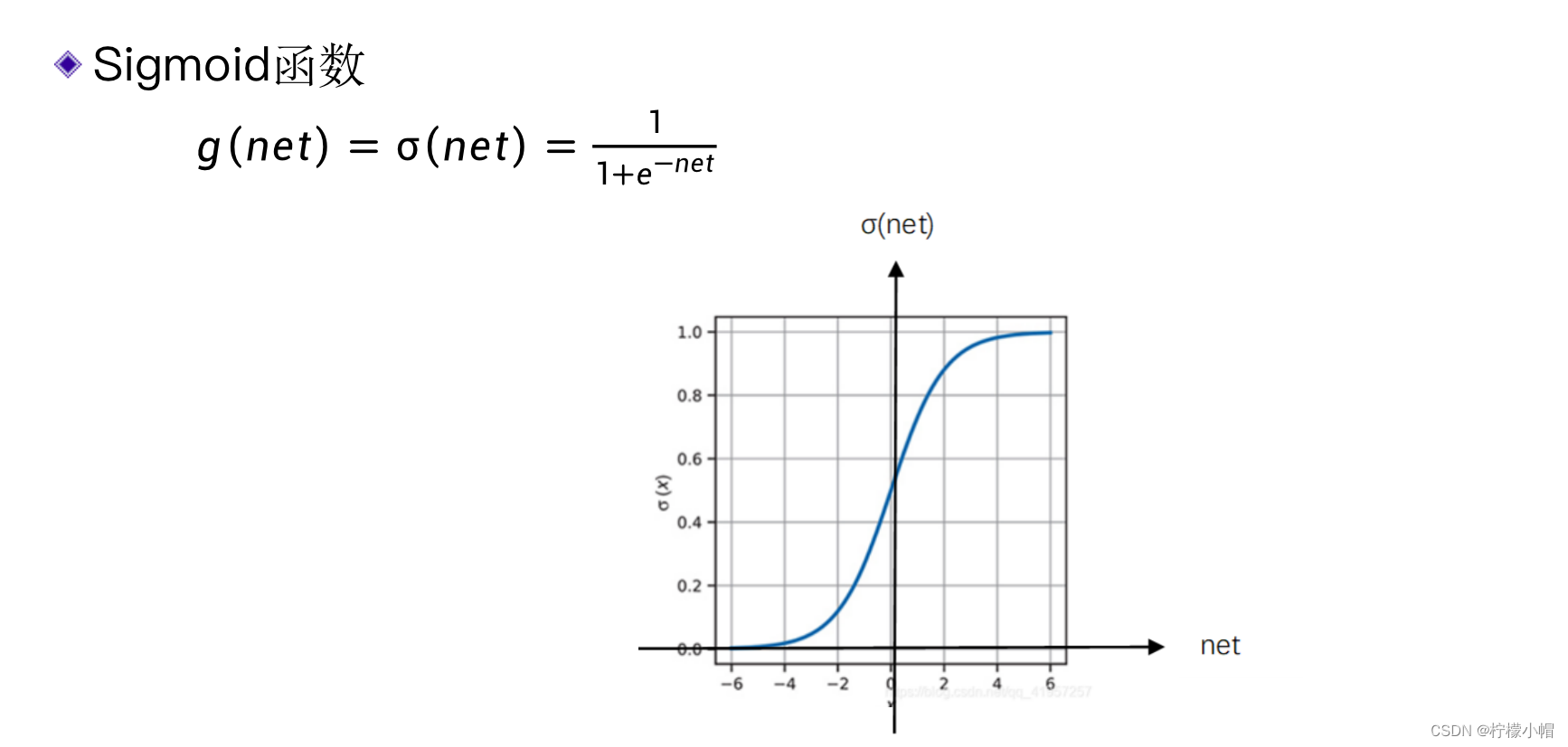
3.3 双曲正切函数

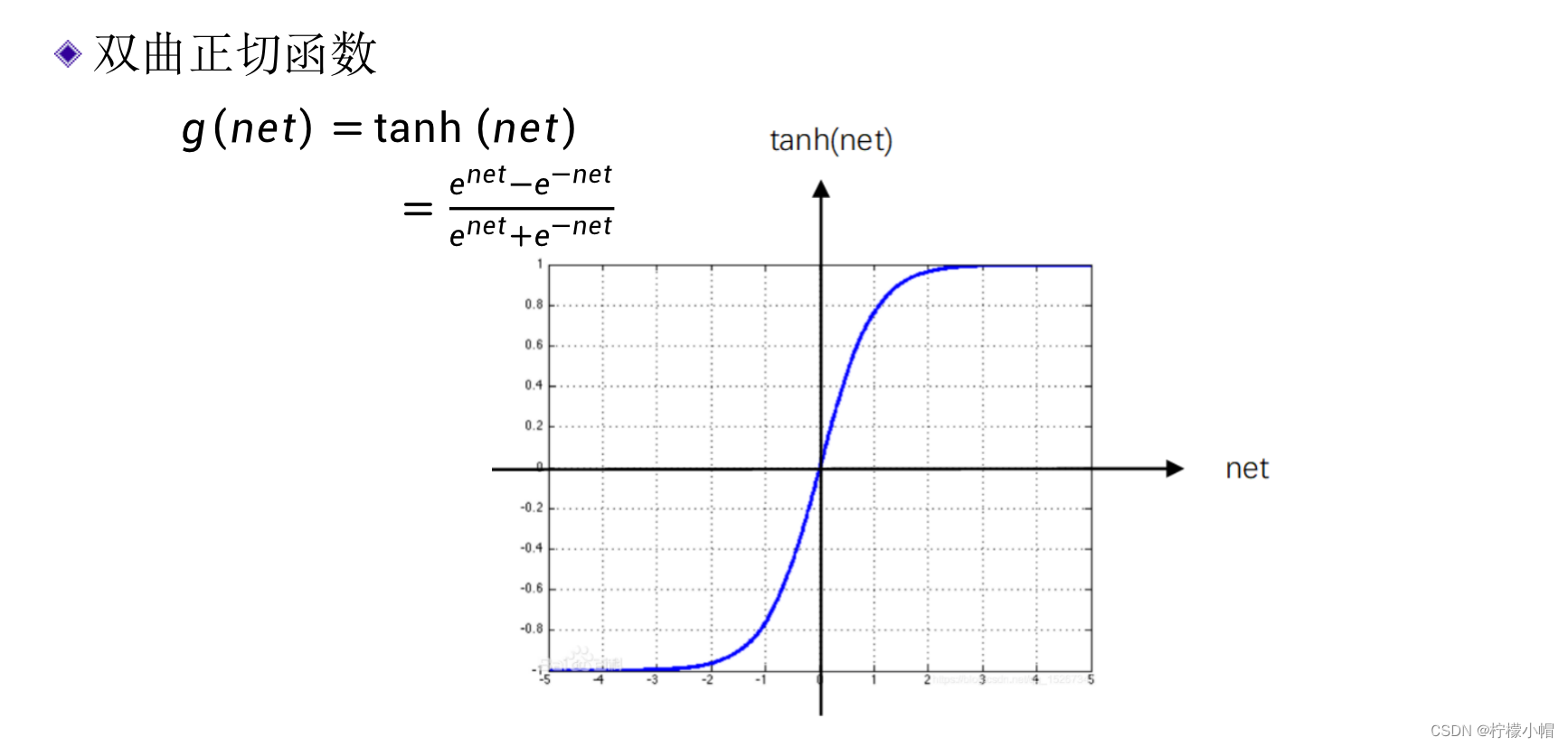
3.4 线性整流函数

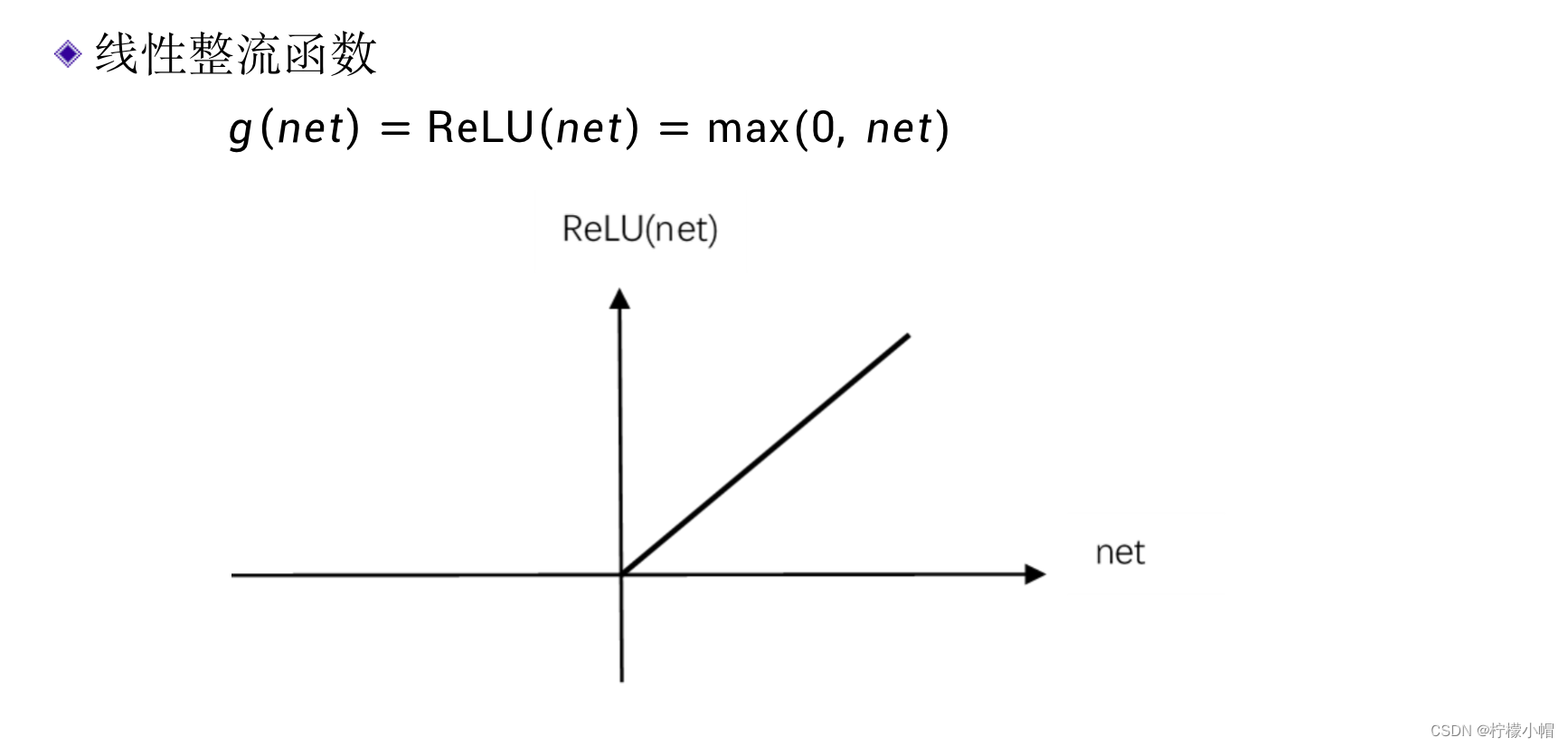
3.5 softmax函数

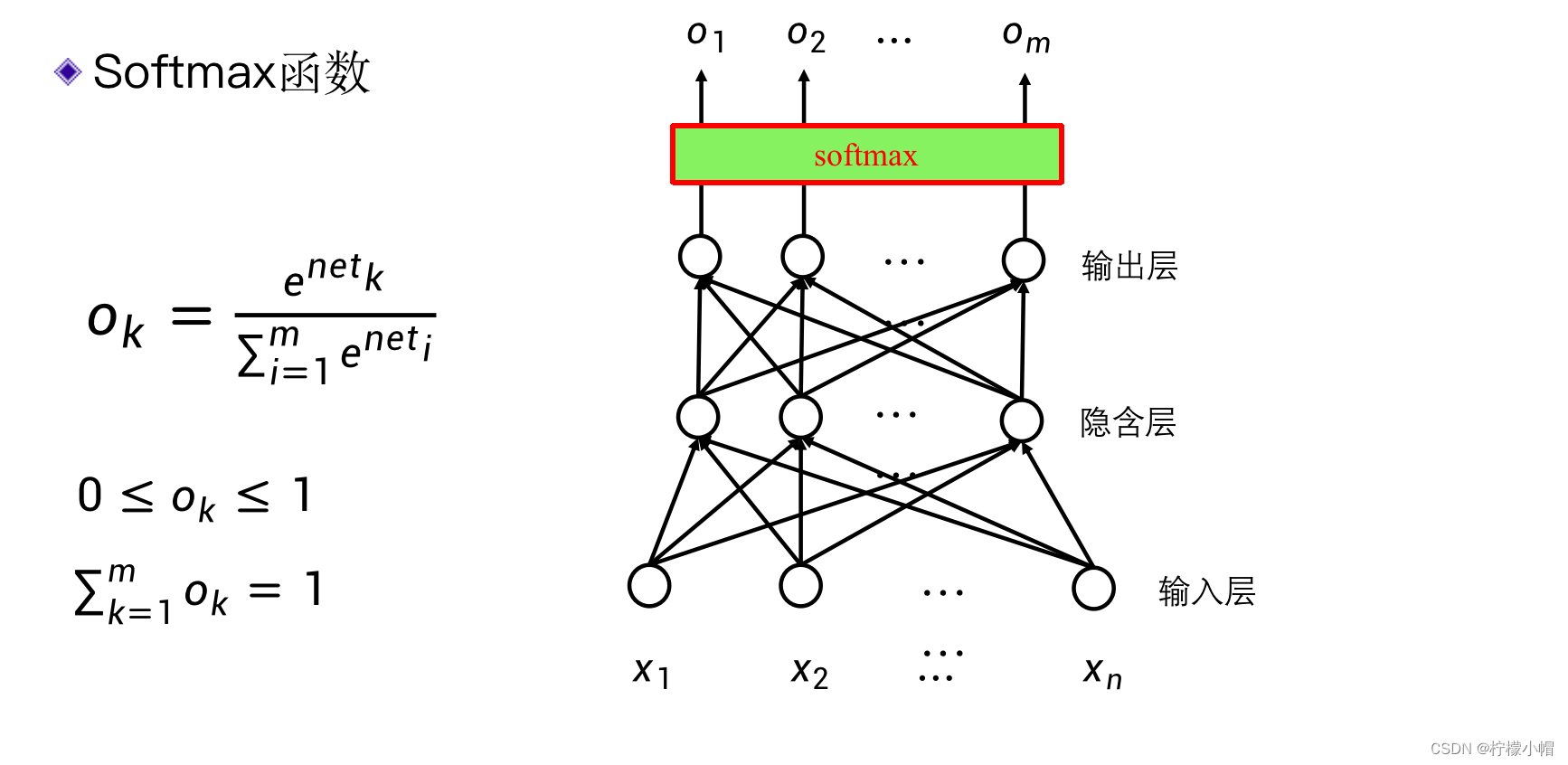
4. 全连接网络

• 多个神经元连接在一起，就组成了一个神经网络。
• 在这个神经网络中，有一个输入层和一个输出层，中间有三个隐含层，每个连接都有一个权重。
• 这个神经网络和上节讲的数字识别神经网络，工作原理是完全一样的。
• 假定这是一个训练好的识别动物的神经网络，并假定第一个输出代表狗、第二个输出代表猫…，当输入一个动物图像时，如果第一个输出接近于1，而其他输出接近于0，则这个动物图像被识别为狗；如果第二个输出接近于1，其他输出接近于0，则这个动物被识别为猫。至于哪个输出代表什么，则是人为事先规定好的。这样的网络可以识别动物，也可以识别花草，也可以识别是哪个人。用什么数据做的训练，就可以做到识别什么，网络结构并没有什么大的变化。
  
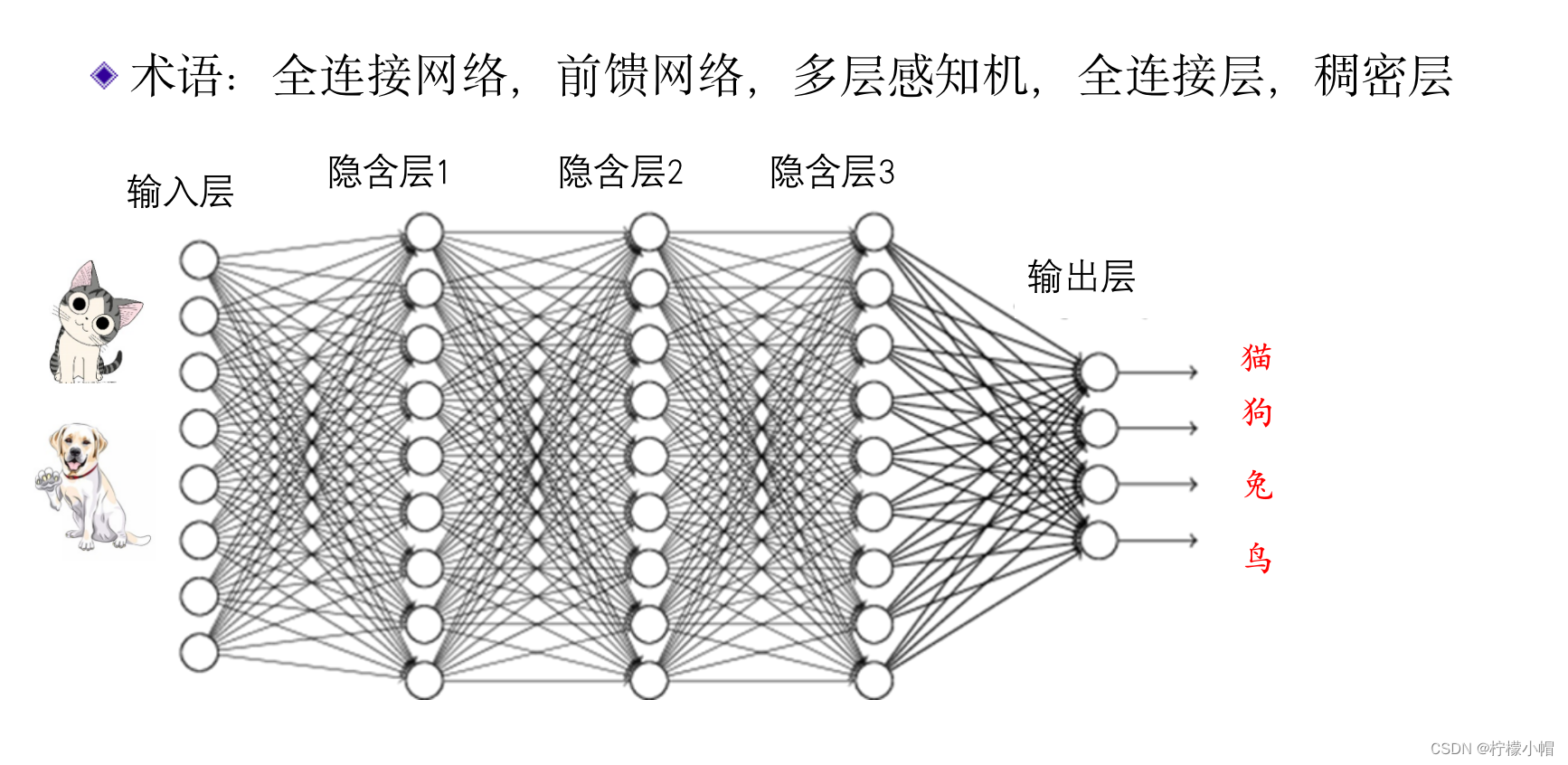
• 相邻的神经元间都有连接，这种神经网络称为全连接神经网络。同时，在计算时，是从输入层一层一层向输出层计算，所以又称为前馈神经网络。

5. 总结

• 一个神经元有n个输入，每个输入对应一个权重，输入与权重的加权和再经过一个激活函数后，得到神经元的输出。
• 激活函数有很多种，常用的包括符号函数、sigmoid函数，双曲正切函数、线性整流函数等。
• 前馈神经网络，又称全连接神经网络，其特点是连接只发生在相邻的两层神经元之间，并且前一层的神经元与下一层的神经元之间，两两均有连接，这也是全连接神经网络名称的来源。由于全连接神经网络均是由输入层开始，一层层向输出层方向连接，所有又称为前馈神经网络。