【数据结构】二叉树的链式存储结构

news2024/11/21 1:28:10

【数据结构】二叉树的链式存储结构

二叉树的存储结构

typedef int BTDataType;
// 二叉树的结构
typedef struct BinaryTreeNode {
    BTDataType data;             // 树的值
    struct BinaryTreeNode *left; // 左孩子
    struct BinaryTreeNode *right;// 右孩子
} BinaryTreeNode;

二叉树的深度优先遍历

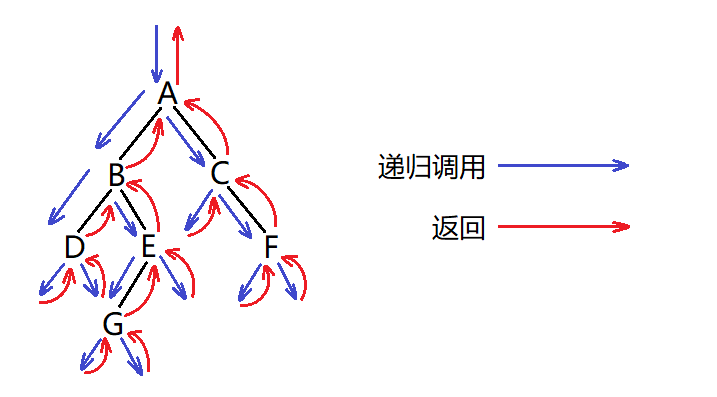
在这里插入图片描述

前序遍历

前序遍历，又叫先根遍历。
遍历顺序：根 -> 左子树 -> 右子树

代码：

// 前序遍历
void BinaryTreePrevOrder(BinaryTreeNode *root) {
    // 前序遍历 根、左子树、右子树
    // 如果root为空，递归结束
    if (root == NULL) {
        printf("NULL ");
        return;
    }

    printf("%d ", root->data);
    BinaryTreePrevOrder(root->left);
    BinaryTreePrevOrder(root->right);
}

中序遍历

中序遍历，又叫中根遍历。
遍历顺序：左子树 -> 根 -> 右子树

代码：

// 中序遍历
void BinaryTreeInOrder(BinaryTreeNode *root) {
    // 中序遍历 - 左子树、根、右子树
    if (root == NULL) {
        printf("NULL ");
        return;
    }
    BinaryTreeInOrder(root->left);
    printf("%d ", root->data);
    BinaryTreeInOrder(root->right);
}

后序遍历

后序遍历，又叫后根遍历。
遍历顺序：左子树 -> 右子树 -> 根

代码：

// 后序遍历
void BinaryPostOrder(BinaryTreeNode *root) {
    // 后序遍历 - 左子树、右子树、根
    if (root == NULL) {
        printf("NULL ");
        return;
    }
    BinaryPostOrder(root->left);
    BinaryPostOrder(root->right);
    printf("%d ", root->data);
}

二叉树的广度优先遍历

层序遍历

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

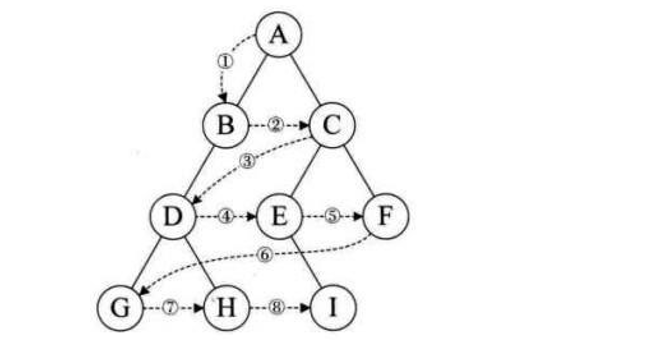
在这里插入图片描述

思路（借助一个队列）：

  1. 先把根入队列，然后开始从队头出数据。
  2. 出队头的数据，把它的左孩子和右孩子依次从队尾入队列（NULL不入队列）。
  3. 重复进行步骤2，直到队列为空为止。

img

特点：借助队列先进先出的性质，上一层数据出队列的时候带入下一层数据。

// 层序遍历 - 利用队列
void BinaryTreeLevelOrder(BinaryTreeNode *root) {
    // 创建一个队列，队列中入数据，取队头，然后带左右子树，出一个数，带一个树的所有子树
    Queue q;
    QueueInit(&q);
    if (root) {
        // root不为NULL，就入队列
        QueuePush(&q, root);
    }

    while (!QueueEmpty(&q)) {
        // 取队头，打印
        BinaryTreeNode *front = QueueFront(&q);
        printf("%d ", front->data);

        // 取完POP
        QueuePop(&q);
        // 取队头，带下一层,
        if (front->left) {
            QueuePush(&q, front->left);
        }

        if (front->right) {
            QueuePush(&q, front->right);
        }
    }
    printf("\n");
    QueueDestroy(&q);
}

二叉树的节点个数

求解树的节点总数时，可以将问题拆解成子问题：

  1. 若为空，则结点个数为0。
  2. 若不为空，则结点个数 = 左子树节点个数 + 右子树节点个数 + 1（自己）。

代码：

// 求二叉树节点个数
int BinaryTreeSize(BinaryTreeNode *root) {
    if (root == NULL) {
        return 0;
    }
    return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

二叉树的叶子节点个数

子问题拆解：

  1. 若为空，则叶子结点个数为0。
  2. 若结点的左指针和右指针均为空，则叶子结点个数为1。
  3. 除上述两种情况外，说明该树存在子树，其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。

代码：

// 求二叉树的叶子节点个数
int BinaryTreeLeafSize(BinaryTreeNode *root) {
    if (root == NULL) {
        return 0;
    }

    if (root->left == NULL && root->right == NULL) {
        return 1;
    }

    return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

第K层节点的个数

思路：
相对于根结点的第k层结点的个数 = 相对于以其左孩子为根的第k-1层结点的个数 + 相对于以其右孩子为根的第k-1层结点的个数。

在这里插入图片描述

代码：

// 求第k层的节点个数 k>=1
int BinaryTreeLevelSize(BinaryTreeNode *root, int k) {
    if (root == NULL) {
        return 0;
    }

    if (k == 1) {
        return 1;
    }

    return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}

值为x的节点

子问题：

  1. 先判断根结点是否是目标结点。
  2. 再去左子树中寻找。
  3. 最后去右子树中寻找。

代码：

// 二叉树查找值为x的节点
BinaryTreeNode *BinaryTreeFind(BinaryTreeNode *root, BTDataType x) {
    if (root == NULL) {
        return NULL;
    }

    if (root->data == x) {
        return root;
    }

    // 左子树递归的节点保存到leftTree中,如果leftTree不为NULL，则return leftTree
    BinaryTreeNode *leftTree = BinaryTreeFind(root->left, x);
    if (leftTree) {
        return leftTree;
    }

    // 右子树递归的节点保存到rightTree中,如果rightTree不为NULL，则return rightTree
    BinaryTreeNode *rightTree = BinaryTreeFind(root->right, x);
    if (rightTree) {
        return rightTree;
    }

    // 找不到，返回NULL
    return NULL;
}

树的高度

子问题：

  1. 若为空，则深度为0。
  2. 若不为空，则树的最大深度 = 左右子树中深度较大的值 + 1。

代码：

// 求二叉树的高度
int BinaryTreeHeight(BinaryTreeNode *root) {
    // 求左子树的高度，右子树的高度
    // 取最大的
    if (root == NULL) {
        return 0;
    }
    int leftHeight = BinaryTreeHeight(root->left);
    int rightHeight = BinaryTreeHeight(root->right);
	
	//如果左右子树两边相等就取左边的高度,所以大于等于
    return leftHeight >= rightHeight ? leftHeight + 1 : rightHeight + 1;
}

判断二叉树是否是完全二叉树

判断二叉树是否是完全二叉树的方法与二叉树的层序遍历类似，但又有一些不同。

思路（借助一个队列）：

  1. 先把根入队列，然后开始从队头出数据。
  2. 出队头的数据，把它的左孩子和右孩子依次从队尾入队列（NULL也入队列）。
  3. 重复进行步骤2，直到读取到的队头数据为NULL时停止入队列。
  4. 检查队列中剩余数据，若全为NULL，则是完全二叉树；若其中有一个非空的数据，则不是完全二叉树。

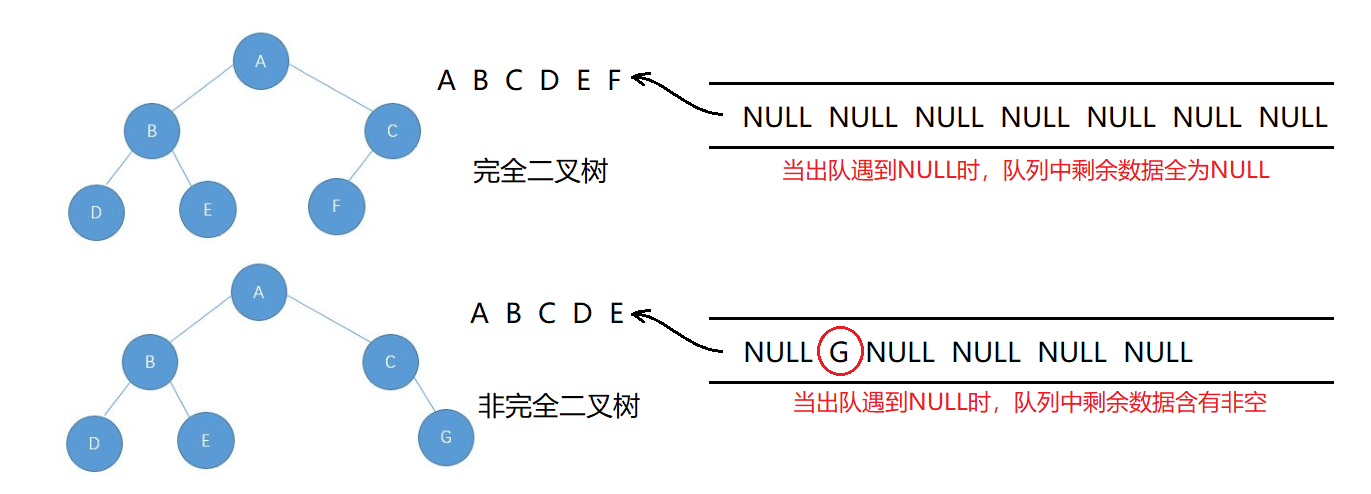
在这里插入图片描述

代码：

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BinaryTreeNode *root) {
    // 层序走，走到第一个为空的时候，就跳出去，如果是满二叉树，后面的节点都应该为空
    Queue q;
    QueueInit(&q);
    if (root) {
        QueuePush(&q, root);
    }

    while (!QueueEmpty(&q)) {
        BinaryTreeNode *front = QueueFront(&q);
        QueuePop(&q);

        if (front == NULL) {
            break;
        } else {
            QueuePush(&q, front->left);
            QueuePush(&q, front->right);
        }
    }
    // 出到空以后，如果后面全是空，则是完全二叉树
    while (!QueueEmpty(&q)) {
        BinaryTreeNode *front = QueueFront(&q);
        QueuePop(&q);
        if (front != NULL) {
            QueueDestroy(&q);
            return false;
        }
    }
    QueueDestroy(&q);
    return true;
}

判断二叉树是否是单值二叉树

单值二叉树，所有节点的值都相同的二叉树即为单值二叉树，判断某一棵二叉树是否是单值二叉树的一般步骤如下：

  1. 判断根的左孩子的值与根结点是否相同。
  2. 判断根的右孩子的值与根结点是否相同。
  3. 判断以根的左孩子为根的二叉树是否是单值二叉树。
  4. 判断以根的右孩子为根的二叉树是否是单值二叉树。

若满足以上情况，则是单值二叉树。

注：空树也是单值二叉树。

代码：

//求单值二叉树
bool isUnivalTree(BinaryTreeNode *root) {
    if (root == nullptr) {
        return true;
    }

    if (root->left && root->data != root->left->data) {
        return false;
    }
    
	if (root->right && root->data != root->right->data) {
        return false;
    }

    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

判断二叉树是否是对称二叉树

对称二叉树，这里所说的对称是指镜像对称：

要判断某二叉树是否是对称二叉树，则判断其根结点的左子树和右子树是否是镜像对称即可。因为是镜像对称，所以左子树的遍历方式和右子树的遍历方式是不同的，准确来说，左子树和右子树的遍历是反方向进行的。

代码：

//求对称二叉树
bool _isSymmetric(BinaryTreeNode *left, BinaryTreeNode *right) {
    // 两个都为NULL，对称
    if (left == NULL && right == NULL)
        return true;

    // 两个其中一个为NULL，一个不为NULL，不对称
    if (left == NULL || right == NULL)
        return false;

    // left的左孩子的值和right的值不相等，不对称
    if (left->data != right->data)
        return false;

    // 左子树的左孩子，和右子树的右孩子对比，然后左子树的右孩子和右子树的左孩子在对比
    return _isSymmetric(left->left, right->right) && _isSymmetric(left->right, right->left);
}

bool isSymmetric(BinaryTreeNode *root) {
    if (root == nullptr) {
        return true;
    }

    return _isSymmetric(root->left, root->right);
}

翻转二叉树

思路：

  1. 翻转左子树。
  2. 翻转右子树。
  3. 交换左右子树的位置。

代码：

BinaryTreeNode *invertTree(BinaryTreeNode *root) {
    if (root == nullptr) {
        return nullptr;
    }

    BinaryTreeNode *leftTree = invertTree(root->left);
    BinaryTreeNode *rightTree = invertTree(root->right);

    root->left = rightTree;
    root->right = leftTree;

    return root;
}

二叉树的构建和销毁

// 申请树节点
BinaryTreeNode *BuyBinaryTreeNode(BTDataType x) {
    BinaryTreeNode *newnode = (BinaryTreeNode *) malloc(sizeof(BinaryTreeNode));
    if (newnode == NULL) {
        perror("malloc fail");
        exit(-1);
    }
    newnode->data = x;
    newnode->left = newnode->right = NULL;
    return newnode;
}

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BinaryTreeNode *BinaryTreeCreate(BTDataType *a, int *pi) {
    if (a[*pi] == '#') {
        (*pi)++;
        return NULL;
    }

    BinaryTreeNode *root = (BinaryTreeNode *) malloc(sizeof(BinaryTreeNode));
    if (root == NULL) {
        perror("malloc fail");
        exit(-1);
    }
    root->data = a[(*pi)++];

    root->left = BinaryTreeCreate(a, pi);
    root->right = BinaryTreeCreate(a, pi);
    return root;
}

销毁：

// 二叉树销毁
void BinaryTreeDestory(BinaryTreeNode **root) {
    if (*root == NULL) {
        return;
    }
    // 后序遍历销毁，根要最后释放
    BinaryTreeDestory(&(*root)->left);
    BinaryTreeDestory(&(*root)->right);
    free(*root);
    *root = NULL;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1000555.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

华为云云服务器云耀L实例评测 | 上手华为云耀L实例：一篇教学文章就够了

华为云云服务器云耀L实例评测 | 上手华为云耀L实例：一篇教学文章就够了

🌷🍁 博主猫头虎（🐅🐾）带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…
阅读更多...
Linux驱动【day2】

Linux驱动【day2】

mychrdev.c: #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include<linux/uaccess.h> #include<linux/io.h> #include"head.h" unsigned int major; // 保存主设备号 char kbuf[128]{0}; unsigned int…
阅读更多...
Stable Diffusion WebUI内存不够爆CUDA Out of memory怎么办？

Stable Diffusion WebUI内存不够爆CUDA Out of memory怎么办？

在我们运行SD的时候，我们经常会爆CUDA Out of memory。 我们应该怎么办呢？ 这是因为我们的显存或者内存不够了。 如果你是用cpu来跑图的则表示内存不够，这个时候就需要换个大点的内存了。 如果你是用gpu来跑图的就说明你显存不够用咯，这时候咋办呢？ 下面我将一一述说…
阅读更多...
企业架构LNMP学习笔记39

企业架构LNMP学习笔记39

MySQL读写分离案例实现&#xff1a; 搭建M-S复制 主从复制的原理&#xff1a;主服务器开启bin-log&#xff08;记录了写操作&#xff09;&#xff0c;从服务器获取到主服务器的bin-log&#xff0c;记录到relay-log中。从服务器在通过异步的线程方式&#xff0c;对于relay-log…
阅读更多...
明星为何会偷税？我国的交税政策是？

明星为何会偷税？我国的交税政策是？

近几年常常会看到某明星偷税漏税塌房的&#xff0c;从最开始的震惊&#xff0c;到后面的习以为常&#xff1a;很多明星都在偷税漏税啊。那么明星为什么会是偷税漏税的高发区&#xff1f; 交税标准 个人 根据我国的税务相关法律规定&#xff0c;个人收入每月超过5000&#xf…
阅读更多...
微服务高可用容灾架构设计

微服务高可用容灾架构设计

导语 相对于过去单体或 SOA 架构&#xff0c;建设微服务架构所依赖的组件发生了改变&#xff0c;因此分析与设计高可用容灾架构方案的思路也随之改变&#xff0c;本文对微服务架构落地过程中的几种常见容灾高可用方案展开分析。 作者介绍 刘冠军 腾讯云中间件中心架构组负责…
阅读更多...
windows本地验证码识别工具

windows本地验证码识别工具

windows本地验证码识别小工具 - 可以用在windows系统中&#xff0c;并可以集成在Java或python程序中 演示视频如下&#xff1a;可用于识别4-7位的字母数字组合的验证码&#xff08;识别准确率在70% - 80%&#xff09;。 验证码识别演示 本项目未开源&#xff0c;如需使用请联…
阅读更多...
IntelliJ IDEA 远程调试 Tomcat

IntelliJ IDEA 远程调试 Tomcat

准备工作 明确远程服务器的 IP 地址&#xff0c;比如我是&#xff1a;192.168.92.128 关掉服务器防火墙&#xff1a;service iptables stop 本地 Remote Server 配置 添加 Remote Server&#xff0c;如下图 复制 Remote Server 自动生成的 JVM 参数&#xff0c;等下有用&…
阅读更多...
透过优衣库秋冬新品巡展，看见服装消费新风尚

透过优衣库秋冬新品巡展，看见服装消费新风尚

这是一个被高温笼罩的夏天&#xff0c;人们想法设法适应季节变换&#xff0c;在这种适应中&#xff0c;尽可能地保持着装之美。 一向走在穿衣风格一线的优衣库&#xff0c;并没有缺席市场更替中涌现的需求&#xff0c;其春夏系列从凉感防晒的功能性服装&#xff0c;到“辣妹T”…
阅读更多...
腾讯云2023年云服务器优惠活动价格表

腾讯云2023年云服务器优惠活动价格表

腾讯云经常推出各种云产品优惠活动&#xff0c;为了帮助大家更好地了解腾讯云服务器的价格和优惠政策&#xff0c;下面给大家分享腾讯云最新云服务器优惠活动价格表&#xff0c;助力大家轻松上云&#xff01; 一、轻量应用服务器优惠活动价格表 1、轻量应用服务器&#xff1a;…
阅读更多...
稳定的 Glance 来了，安卓小部件有救了！

稳定的 Glance 来了，安卓小部件有救了！

稳定的 Glance 来了&#xff0c;安卓小部件有救了&#xff01; 稳定版本的 Glance 终于发布了&#xff0c;来一起看看吧&#xff0c;看看这一路的旅程&#xff0c;看看好用么&#xff0c;再看看如何使用&#xff01; 前世今生 故事发生在两年的一天吧&#xff0c;其实夸张了…
阅读更多...
数据结构算法刷题（29）动态规划

数据结构算法刷题（29）动态规划

思路一&#xff1a;回溯&#xff1a;按照选和不选的判断方式&#xff0c;使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…
阅读更多...
医疗环境升级改造，从此温湿度监控不用慌！

医疗环境升级改造，从此温湿度监控不用慌！

在现代医疗环境中&#xff0c;为了确保患者的舒适和康复&#xff0c;温度和湿度的监控和管理变得至关重要。特别是在疗养院这样的医疗机构中&#xff0c;患者的健康与室内环境条件密切相关。温度和湿度的不适当波动可能导致不仅是不适&#xff0c;还可能加剧病情&#xff0c;影…
阅读更多...
9月8日上课内容 第一章 rsync远程同步

9月8日上课内容 第一章 rsync远程同步

主从复制总结 redis主从复制 是为了数据冗余和读写分离 在这两种模式中&#xff0c;有两种角色主节点 (master) 和从节点 (slave) &#xff0c;主节点负责处理写的操作&#xff0c;并将数据更改复制到一个或多个从节点。这样我们的主节点负载减轻&#xff0c;从节点可以提供数据…
阅读更多...
UI设计新手指南之什么是UI设计？

UI设计新手指南之什么是UI设计？

最直观的&#xff0c;只要用手机&#xff0c;打开界面就会接触到 UI 设计。 UI 设计是什么&#xff1f;它是指对软件人机交互、操作逻辑、界面美观的整体设计。UI设计的目的是创造出简单、直观、易于使用的界面&#xff0c;为用户提供良好的体验。随着移动互联网的兴起&#x…
阅读更多...
分享一下奶茶店怎么在小程序上做商城功能

分享一下奶茶店怎么在小程序上做商城功能

随着移动互联网的普及&#xff0c;越来越多的消费者倾向于在手机上完成购物需求。对于奶茶店来说&#xff0c;在小程序上开设商城功能不仅可以扩大销售渠道&#xff0c;还能提高品牌知名度和用户体验。本文将探讨如何在小程序上为奶茶店实现商城功能。 对于奶茶店的商城功能&am…
阅读更多...
Spring-MVC使用JSR303及拦截器，增强网络隐私安全

Spring-MVC使用JSR303及拦截器，增强网络隐私安全

目录 一、JSR303 ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 常用注解 ( 4 ) 入门使用 二、拦截器 2.1 是什么 2.2 拦截器与过滤器的区别 2.3 应用场景 2.4 基础使用 2.5 用户登录权限控制 给我们带来的收获 一、JSR303 ( 1 ) 是什么 JSR 303是Java规范请求&#xff…
阅读更多...
旅游复苏弹高OTA业绩，未来走势却有“U型曲线”与“抛物线”之变

旅游复苏弹高OTA业绩，未来走势却有“U型曲线”与“抛物线”之变

文 | 螳螂观察 作者 | 易不二 经历了3年蛰伏&#xff0c;旅游业确实熬出头了&#xff0c;OTA也迎来了强势反弹。 自年初起就逐步恢复的旅游行业&#xff0c;经历了暑期小高潮后&#xff0c;正在逐步以强劲的复苏能力&#xff0c;为OTA们的期中财报增彩。 今年二季度&#x…
阅读更多...
83 # 静态服务中间件 koa-static 的使用以及实现

83 # 静态服务中间件 koa-static 的使用以及实现

静态服务中间件&#xff1a;koa-static 中间件可以决定是否向下执行&#xff0c;如果自己可以处理&#xff0c;那么直接处理完毕结束&#xff0c;如果自己处理不了&#xff0c;next 方法会继续向下执行 新建 public 文件夹&#xff0c;里面添加 index.html、style.css 文件 …
阅读更多...
机器学习_个人笔记_周志华(更新中......)

机器学习_个人笔记_周志华(更新中......)

第1章 绪论 1.1 引言 形成优秀的心理表征&#xff0c;自然能成为领域内的专家。 系统1 & 系统2。 机器学习&#xff1a;致力于研究如何通过计算的手段&#xff0c;利用经验来改善系统自身的性能。主要研究计算机从数据中产生model的算法&#xff0c;即“learning algori…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023